Взаимное положение прямых.
Ответ:
Прямые в пространстве могут быть параллельными, пересекаться и скрещиваться.
И
сходя
из одного из инвариантных свойств
ортогонального проецирования: их
одноименные проекции параллельны между
собой. Если прямая АВ параллельна
прямой CD,
то, образуя вместе со своими проекциями
плоскости перпендикулярные горизонтальной
плоскости проекций, они
дадут ав параллельно сd (рис.
19)
Параллельные прямые лежат в одной плоскости.
Пересекающиеся прямые
Е
сли
прямые пересекаются, то они имеют одну
общую точку (рис.20).
Исходя из одного из инвариантных свойств ортогонального проецирования, если прямые в пространстве пересекаются, то их проекции пересекаются в точках, лежащих на одном перпендикуляре к оси (на одной проекционной линии связи их разделяющей). Это положение безусловно только для прямых общего положения.
Так
как, прямые
пересекаются, то точка К –
общая для двух прямых, а исходя из
свойства принадлежности точки прямой,
проекции точки должны лежать на одном
перпендикуляре к оси.
Скрещивающиеся прямые
Такие прямые не параллельны и не пересекаются между собой.
Проекции таких прямых могут пересекаться, но точки пересечения проекций не находятся на одном перпендикуляре к оси
Точки пересечения проекций у скрещивающихся прямых называются конкурирующими. В действительности конкурирующие точки принадлежат разным прямым.
Конкурирующие точки дают возможность судить о положении прямых друг относительно друга в пространстве, а именно используются для определения видимости ребер гранных геометрических тел ( призм, пирамид ) на отдельных плоскостях проекций. Каждая проекция представляет собой проекции двух точек, из которых одна принадлежит первой прямой, а другая – второй.
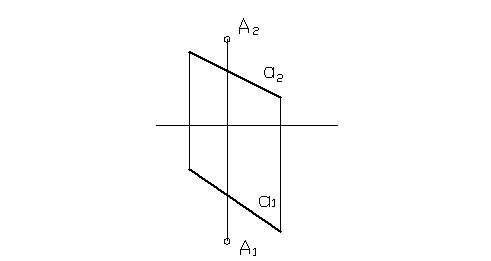
Комплексный чертеж плоскости. Плоскости общего и частного положения.
Плоскость задается несколькими способами:
а
)
три
точки, не лежащие на одной прямой;
б) прямая и точка, не лежащая на ней;
в) две параллельные прямые;
г) две пересекающиеся прямые;
д
)
плоская фигура (многоугольник, круг и
т.д.)
П
лоскости
частного положения аналогично прямой
подразделяются на плоскости уровня и
проецирующие плоскости. На рисунке 19
(а,б,в) изображены, соответственно,
горизонтальная, фронтальная и профильная
плоскости. Причём горизонтальная
плоскость задана двумя параллельными
прямыми, фронтальная и профильная
плоскости – двумя пересекающимися
прямыми.
На рисунке 20 (а,б,в) показаны проецирующие плоскости. Горизонтально-проецирующая (рис. 20а) задана треугольником, фронтально-проецирующая (рис. 20б) - параллельными прямыми и профильно-проецирующая (рис. 20в) – пересекающимися прямыми.
Условие принадлежности точки и прямой плоскости.
Ответ:
Точка принадлежит прямой, если её проекции лежат на одноимённых проекциях этой прямой;
Точка принадлежит плоскости, если она лежит на прямой, лежащей в этой плоскости;
П
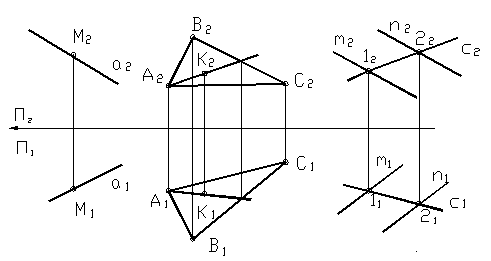рямая
принадлежит плоскости, если она проходит
через две точки, лежащие в этой плоскости;
Взаимное положение прямой и плоскости.
Ответ:
Возможны следующие случаи взаимного расположения прямой и плоскости:
1
)
Прямая пересекает плоскость, то есть:
d ∩α = N. В этом случае прямая и плоскость
имеют одну общую точку.
2
)
Прямая параллельна плоскости, то есть:
d || α. В этом случае прямая и плоскость
не имеют общих точек.
3
)
Прямая лежит в плоскости, то есть: d 
α.
В этом случае прямая и плоскость имеют
бесчисленное множество общих точек.
Образование поверхности. Определитель поверхности.
Ответ:
Все поверхности можно подразделить на графические, и геометрические.
Часть пространства, ограниченная со всех сторон поверхностью, называется телом.
Геометрические поверхности могут быть образованы движением в пространстве прямой или кривой линии, которая называется образующей.
линейчатые поверхности, которые могут быть образованы движением в пространстве прямой линии ;
циклические поверхности, которые могут быть образованы движением в пространстве окружности ;
поверхности вращения, которые могут быть образованы движением какой либо линии вокруг закрепленной оси;
винтовые поверхности, при образовании которых хотя бы одна точка образующей совершает винтовое движение.
Совокупность геометрических элементов, которая будучи заданной позволяет реализовать закон образования поверхности, называется определителем поверхности.
Определитель состоит из графической и алгоритмической части.
• Определитель вполне задает поверхность на чертеже.
• В общем случае поверхность считается заданной, если относительно любой точки пространства можно ответить на вопрос: принадлежит или нет данная точка поверхности.
Обычно определитель и закон образования поверхности представляют в определенной знаковой записи, которую называют формулой поверхности.
На практике из всех возможных способов образования поверхности выбирают наиболее простой.
При кинематическом способе задания поверхность рассматривается как совокупность всех положений движущейся линии. Этот способ задания поверхности является предпочтительным в инженерной графике. В инженерной графике поверхность рассматривают как множество всех последовательных положений движущейся линии. Эта линия называется образующей l. |
|
• Закон перемещения образующей обычно определяется другими линиями, по которым перемещается образующая при своем движении. • Эта линия называется направляющей m. |
|
В зависимости от формы образующей все поверхности можно разделить на линейчатые, у которых образующая прямая линия, и нелинейчатые, у которых образующая кривая линия.
В линейчатых поверхностях выделяют поверхности развертывающиеся, совмещаемые всеми своими точками с плоскостью без разрывов и складок, и неразвертывающиеся, которые нельзя совместить с плоскостью без разрывов и складок.