1.3. Классификация видов плазмы

С помощью введенных понятий о дебаевской длине и плазменной частоте можно классифицировать встречающиеся в природе плазмы на разреженные и плотные, классические и квантовые. Внутренняя энергия плазмы складывается из кинетических энергий ионов и электронов и из энергии их электростатического новского взаимодействия (в плазме, нагретой до релятивистских температур, нужно учитывать и магнитное взаимодействие). Сравним среднюю кинетическую энергию (3/2)T, приходящуюся на одну частицу, со средней энергией взаимодействия. Из-за дебаевского экранирования взаимодействие заряженной частицы с далекими частицами несущественно, и надо учитывать в основном лишь ближайших соседей. Среднее расстояние до соседней частицы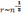 , следовательно, энергия взаимодействия приблизительно равна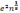 . Поэтому, как правило, плазму можно считать идеальным газом, если 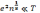. Если обе части неравенства возвести в степень 3/2, то, как легко заметить, неравенство примет следующий вид: . 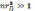Таким образом, условие идеальности плазмы можно записать через число частиц в объеме с размерами порядка дебаевской длины. Это число должно быть много больше единицы. При тепловая энергия частиц превышает как энергию электростатического взаимодействия, так и равновесную энергию электронных колебаний плазмы. Если указанное условие не выполнено, плазма уже не является газом, а скорее напоминает жидкость с, вообще говоря, очень сложным и до сих пор неизвестным уравнением состояния. При дальнейшем повышении плотности плазмы можно ожидать ее металлизации. При больших плотностях в плазме должны проявляться также и квантовые эффекты. Сначала их следует учитывать в ленгмюровских колебаниях. Очевидно, это должно произойти тогда, когда квант энергии плазменных колебаний станет сравнимым со средней тепловой энергией, приходящейся на один электрон. При этом условии длина волны де-Бройля для электронов со скоростями порядка средней тепловой оказывается сравнимой с дебаевским радиусом. Еще раньше, когда будет выполнено условие, т. е. длина волны де-Бройля будет сравнима со средним расстоянием между электронами, квантовой становится статистика электронов (распределение Ферми — Дирака вместо больцмановского). Это так называемая квантовая вырожденная плазма.

Согласно принципу Паули два электрона с одинаковыми спинами не могут находиться в одной и той же точке пространства, поэтому потенциальная энергия взаимного электростатического отталкивания электронов, а значит, и возвращающая сила в плазменных колебаниях несколько уменьшаются. Однако, поскольку обменные силы короткодействующие, они не могут изменить частоту ленгмюровских волн с бесконечной длиной волны и влияют лишь на частоту волн с конечной величиной волнового вектора.

Подавляющее большинство плазм в природе можно считать идеальным газом (космическая, газоразрядная и т. п.). Примером неидеальной плазмы могут служить сильные электролиты. Наиболее интересными из них являются растворы щелочных металлов в аммиаке, где хорошо прослеживается переход к жидкому плазменному состоянию и металлизации. Представителем квантовой плазмы молено считать электронный газ в металлах: при плотности конденсированного вещества (n_e~10²³ см^-3) квант энергии плазменных колебаний по порядку величины оказывается равным единицам электронвольт. Квантовыми свойствами может обладать и плазма, состоящая из электронов и положительно заряженных квазичастиц — дырок в полупроводниках. Виды плазмы такого рода принято объединять под названием плазма твердого тела. Явление квантового вырождения должно иметь место и для электронного газа в очень плотном веществе звезд — белых карликов.

Свойства плазмы усложняются, если одновременно с заряженными частицами (ионами и электронами) в ней существуют также нейтральные атомы и молекулы, т. е. плазма не является полностью ионизованной.

Степень ионизации плазмы — отношение числа заряженных частиц к первоначальному числу атомов—определяется конкуренцией между процессами ионизации (развала атомов) и обратным процессом рекомбинации, т. е. воссоединения электронов и ионов в нейтральные частицы.

Общепринято также делить плазму на высоко- и низкотемпературную. Это разделение в значительной степени связано с видами конкретных исследований и их приложений. Так, с высокотемпературной плазмой связаны исследования по проблеме управляемого термоядерного синтеза. Именно эти исследования стимулировали бурный расцвет физики высокотемпературной плазмы в 50—60-х годах, позволивший объяснить многие явления в физике радиационных поясов, и в некоторых новых областях астрофизики. Низкотемпературная плазма является рабочим телом— газообразным проводником для магнитогидродинамических генераторов.

Холодную плазму в ионосфере можно рассматривать как одну из природных форм реализации низкотемпературной плазмы. Изложенную классификацию плазм удобно

проиллюстрировать диаграммой (рис. 1.3). Поскольку интересы авторов относятся, главным образом, к большим Т, книга практически посвящена физике горячей, полностью ионизованной плазмы.

Широкое использование численных методов в физике плазмы, первоначально служившее подспорьем при анализе экспериментов, и их сопоставлении с теорией, сейчас привело к самостоятельному направлению, имеющему дело с так называемой численной плазмой. Прямые решения на быстродействующих вычислительных машинах уравнений движения N взаимодействующих заряженных частиц часто называют численными экспериментами. В некоторых случаях N удается довести до 10⁶.

(источник:Арцимович Л.А., Сагдеев Р.З. Физика плазмы для физиков, гл.1, §1.3)

2. Виды плазменных состояний. Идеальная и неидеальная плазма. Параметр вырождения. (см. 1.3) Изотермичная и неизотермичная плазма. Обобщенное понятие температуры. Газовое приближение плазмы. Частично и полностью ионизированная плазма. Степень ионизации плазмы. (см. 1.3) Замагниченная и незамагниченная плазма. Параметр ωτ. (см. 4.7) Магнитное давление.