7.6. Проводимость плазмы

Для простейшего случая постоянного тока в однородной плазме уравнение обобщенного закона Ома (16.18) принимает вид

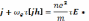(17.1)

где

(17.2)

электронная циклотронная частота; h — единичный вектор в направлении магнитного поля.

При отсутствии магнитного поля или для составляющей тока вдоль его направления векторное произведение [jH] выпадает, и из уравнения (17.1) получается нормальная или продольная проводимость плазмы

(17.3)

Для нахождения поперечной проводимости расписываем уравнение (17.1) в составляющих. Если направить ось z вдоль магнитного поля, то

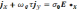(17.4)

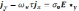(17.5)

Поперечная проводимость плазмы есть величина тензорная. Проще всего выразить соотношения (17.3)—(17.5) с помощью тензора сопротивления R, определяемого соотно- соотношением

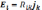(17.6)

Компоненты этого тензора образуют таблицу (матрицу):

(17.7)

Обычно принято вместо тензора сопротивления пользоваться тензором проводимости, который определяется равенством

(17.8)

Чтобы найти компоненты этого тензора, нужно найти матрицу, обратную (17.7), т. е. решить систему уравнений (17.4)—(17.5) относительно составляющих тока. В данном случае достаточно умножить одно из уравнений на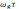 , прибавить ко второму или вычесть из него, чтобы получить

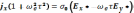(17.9)

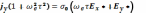
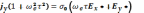(17.10)

Отсюда тензор проводимости однородной плазмы для постоянного тока имеет вид:

(17.11)

В явном виде составляющие тока выражаются формулами:

(17.12)

(17.13)

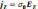(17.14)

Для замагниченнои плазмы — большое число. В этом случае поперечная проводимость должна быть гораздо меньше продольной и уменьшаться обратно пропорционально квадрату циклотронной частоты, т. е. квадрату напряженности магнитного поля. Ток должен течь не только вдоль электрического поля, но и поперек него (холл-эффект), причем в замагниченнои плазме при скрещенных полях ток поперек электрического поля (холловский ток) должен быть гораздо больше, чем ток вдоль электрического, но поперек магнитного поля, и уменьшаться только как первая степень напряженности магнитного поля. В реальных условиях проводимость плазмы сильно осложняется пространственной неоднородностью, вызывающей электрические поля поляризации, а также дрейфовые токи и ток намагничивания.

(источник: Д.А. Франк-Каменецкий, Лекции по физике плазмы, гл. 1, §§7-8)

7.7. Классическая и бомовская диффузия

Е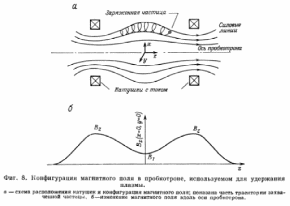 сли в нейтральном газе создается градиент плотности, то может возникнуть поток частиц, стремящийся уменьшить этот градиент. Такой процесс называется диффузией, причем в нейтральном газе этому процессупрепятствуют столкновения. Наоборот, в плазме столкновения иногдамогут способствовать диффузии. В плазме для ограничения свободного движения частиц (которое и приводит к диффузии в неоднородных нейтральныхгазах) часто используют магнитные поля. На фиг. 8показана подобная конфигурация магнитного поля. Однако теперь столкновения между частицамиприводят к их смещению поперек магнитного поля и, таким образом, способствуют диффузии.

Поток частиц Г через единичную площадь в единицу времени равенпроизведению плотности частиц на их среднюю скорость. Поток частиц,вызванный наличием градиента плотности, пропорционален коэффициенту диффузии D, определяемому следующим образом

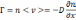
(18.1)

В силу электрических свойств плазмы коэффициент диффузии плазмы,состоящей из ионов и электронов, даже в отсутствие магнитных полей отличается от классического коэффициента диффузии газа. Например, при диффузии редкой плазмы в плотном нейтральном газе более подвижные электроны стараются опередить ионы. При этом возникает электрическое поле,связанное с разделением зарядов, которое тормозит диффузию электронови увеличивает диффузию ионов, поддерживая зарядовую нейтральность.Увеличенная диффузия ионов совместно с электронами называется амбиполярной диффузией. Коэффициент амбиполярной диффузии плазмы с одинаковой температурой электронов и ионов в два раза превышает коэффициентсвободной диффузии одних ионов, т. е.

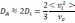(18.3)

здесь ν_c — частота столкновений ионов с нейтральными частицами.

Постоянное магнитное поле заставляет заряженные частицы двигатьсяпо винтовым траекториям. Если имеется поперечный градиент плотностичастиц в магнитном поле, то в результате столкновений между собой электроны и ионы будут диффундировать поперек магнитного поля. Коэффициентдиффузии в этом случае имеет вид

(18.4)

Это выражение показывает, что коэффициент свободной диффузии уменьшается пропорционально 1/B²и возрастание частоты столкновений приводитк увеличению диффузии. Уменьшение диффузии поперек силовых линиймагнитного поля, пропорциональное 1/В², позволяет предположить, чтосильные магнитные поля дадут возможность удерживать плазму в течениедлительного времени. К сожалению, большинство экспериментов по магнитному удержанию плазмы указывает на то, что скорость диффузии превышает значение, предсказываемое выражением (18.4), если ν_c определяется через сечение парных столкновений. Более того, эксперименты показывают, что коэффициент диффузии даже не пропорционален 1/В². Диффузияплазмы с коэффициентом, пропорциональным 1/B, получила названиебомовской диффузии по имени американского физика Бома, который предположил, что коллективные процессы в плазме, такие, как неустойчивости,могут привести к диффузии с коэффициентом

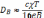(18.5)

Это выражение для коэффициента диффузии было предположено, а не выведено теоретически. Однако можно сказать, сравнивая (18.2) и (18.4),что скорость ухода заряженных частиц поперек магнитного поля максимальна при ν_c≈ω_c. Считая, что ν_c принимает это оптимальное значение, мыполучаем бомовскую диффузию. Бом, по-видимому, предполагал, что увеличение эффективной частоты столкновений вплоть до этого значения вызывается наличием неустойчивости. Когда ν_c=ω_c, частица благодаря столкновениям в среднем проходит поперек магнитного поля за каждый циклотронный период расстояние, равное ее ларморовскому радиусу (а_L = v/ω_c).В тех работах, которые касаются экспериментов по магнитному удержаниюплазмы, время удержания приводят в единицах бомовского времени, т. е.экспериментальное значение коэффициента диффузии делится на коэффициент бомовской диффузии.

П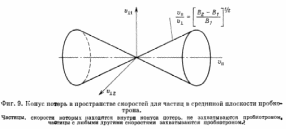 омимо только что описанной диффузии в конфигурационном пространстве, имеется также диффузия в пространстве скоростей. Диффузия подобного рода также происходит вследствие столкновений частиц друг с другоми направлена в сторону уменьшения любой анизотропии или других характеристик функции распределения по скоростям, невыгодных с точки зренияэнтропии. Например, диффузия в пространстве скоростей происходит в плазме, помещенной в магнитное поле пробкотрона (фиг. 8 и 9). Частицы захватываются в этой конфигурации магнитных полей, если их скорости лежатвне конуса потерь пробкотрона, т. е. в срединной плоскости ловушки:

Частицы, скорости которых находятся внутри конуса потерь, проходятнасквозь через область максимального магнитного поля, в то время какчастицы со скоростями вне конуса потерь захватываются. При отсутствиистолкновений они могли бы оставаться захваченными в ловушке бесконечно долго. В результате столкновений координаты каждой данной частицыв пространстве скоростей меняются со временем случайным образом.Траектория случайного блуждания такой частицы в пространстве скоростей приводит ее, в конце концов, внутрь конуса потерь. При следующем попаданиив область В₂ частица выходит из ловушки. В этом примере частицы не диффундируют поперек силовых линий, но за счет изменения своей скоростивыходят из пробкотрона, оставаясь на одной и той же силовой линии. Неустойчивости также могут вызвать диффузию в пространстве скоростей.Например, рассмотрим функцию распределения для встречных пучков частиц, такую, как показано на фиг. 10. Эта функция распределения неустойчива, в результате чего в плазме возбуждаются различные типы волн, чтоприводит к диффузии частиц в пространстве скоростей в направлениях, указанных стрелками на фиг. 10, т. е. в направлении более устойчивой функции распределения. Если энергия волн остается малой, процесс, вызывающий такую диффузию, называется слабой турбулентностью. Слабая турбулентность широко изучалась, причем оказалась доступной достаточноглубокому анализу.

(источник: Н.Кролл, А.Трайвелпис, Основы физики плазмы, гл.1, §14)