7.2. Идеальная проводимость и дрейфовое движение

Во многих задачах от приближения магнитной гидродинамики можно перейти к еще более упрощенному способу рассмотрения плазмы, устремив проводимость σк бесконечности. Такое рассмотрение носит название приближения идеальной проводимости. При бесконечной проводимости сколь угодно малое электрическое поле вызывало бы бесконечный ток, что требовало бы бесконечно большой затраты энергии, и потому невозможно. Следовательно, в приближении идеальной проводимости электрическое поле в системе координат, связанной с плазмой (такую систему иногда называют сопутствующей), должно равняться нулю

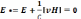(13.1)

или

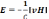(13.2)

Векторное произведение [vH] зависит только от составляющей скорости, перпендикулярной к магнитному полю, которую мы будем обозначать v_⊥. Поэтому выражение (13.2) можно записать в виде

(13.2а)

поскольку результат от этого не изменится. Таким образом, условие (13.2) накладывает определенное требование на скорость движения плазмы поперек магнитного поля v_⊥; скорость вдоль магнитного поля v_|| может иметь любое значение. Чтобы получить значение v_⊥, достаточно умножить выражение (13.2а) векторно на Н справа. Получаем

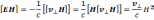(13.3)

так как скалярное произведение 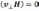. Из равенства (13.3)

(13.4)

В скрещенных магнитном и электрическом полях идеально проводящая среда должна двигаться со скоростью, определяемой формулой (13.4). Такое движение называется дрейфом, а скорость, выражаемая формулой (13.4), —дрейфовой скоростью. Когда мы будем рассматривать движение заряженных частиц в плазме, то ознакомимся еще с рядом разновидностей дрейфового движения. Но только для дрейфа в скрещенных магнитном и электрическом полях скорость дрейфа одной частицы совпадает со скоростью дрейфа плазмы как целого. Этот вид дрейфового движения называется электрическим дрейфом в отличие от других видов дрейфа, при которых частицы разных зарядов движутся, как мы увидим, в противоположных направлениях. Как видно из формулы (13.4), скорость электрического дрейфа направлена перпендикулярно к плоскости, в которой лежат векторы магнитного и электрического полей. В формуле (13.4) величина векторного произведения [ЕН] зависит только от составляющей электрического поля, перпендикулярной к магнитному; эту составляющую мы будем обозначать E_⊥. Поэтому формулу (13.4) можно записать в виде

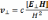(13.4a)

Параллельная магнитному полю составляющая электрического поля не влияет на скорость дрейфа плазмы как целого поперек поля; она вызывает ток, текущий вдоль магнитного поля. Величина дрейфовой скорости выражается как

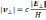(13.5)

Пользоваться выражением дрейфовой скорости в векторной форме нужно только для того, чтобы определить ее направление при данных направлениях магнитного и электрического полей. Из формулы (13.4а) следует, что если магнитное поле направлено к нам, а перпендикулярная к нему составляющая электрического поля вверх, то плазма должна дрейфовать вправо. При приближенном рассмотрении поведения плазмы в магнитном поле удобно пренебречь электрическим сопротивлением плазмы, т. е. рассматривать ее как идеально проводящую среду. Согласно только что сказанному, движение плазмы в этом приближении будет иметь дрейфовый характер. Поэтому такое приближение и называется дрейфовым приближением.