6.1. Тепловая и кулоновская энергия плазмы

Для равновесной плазмы тепловая энергия выражается так же, как для идеального газа. В полностью ионизированной плазме плотности тепловой энергии

где n — концентрация частиц; Т — температуры в энергетических единицах. В частично ионизованной плазме добавляется энергия нейтральных частиц (атомов и молекул), определяемая по обычным формулам термодинамики газов. В термодинамическом отношении плазма отличается от идеального газа тем, что кроме тепловой энергии в ней может оказаться существенной еще и энергия электростатического взаимодействия. Если взаимодействие не слишком сильное, то энергия взаимодействия может быть оценена в приближении Дебая. Изменение потенциала вследствие взаимодействия для частицы с зарядом Ze выражается как

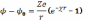
малых расстояниях r разложение в ряд дает

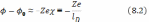
Высшие члены при исчезают. Таким образом, электростатическое взаимодействие создает в точке, где находится каждая частица, добавочный отрицательный потенциал (8.2).

Этот потенциал происходит от притяжения частицы окружающей ее «атмосферой» с избытком частиц противоположного знака. Он равен численно кулоновскому потенциалу, возбуждаемому частицей на расстоянии, равном длине экранирования. Если умножить добавочный потенциал на заряд частицы и просуммировать по всем частицам, находящимся в единице объема, то мы каждую пару частиц учтем дважды. Поэтому полная плотность электростатической энергии

Она такова, как если бы все частицы притягивались между собой на длине, равной длине экранирования 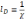. В силу квадратичности по Z формулы (8.3) кулоновская энергия плазмы всегда отрицательна, т. е. имеет такой знак, как энергия притяжения. Это объясняется тем, что каждая заряженная частица создает вокруг себя атмосферу с преобладанием зарядов противоположного знака, к которой частица притягивается. Таким образом, полная энергия плазмы всегда меньше, чем энергия идеального газа. Подстановка значения 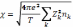дает

или, вводя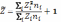

Сопоставляя с , находим, что плотность кулоновской энергии

Полезно рассмотреть сферу с радиусом, равным длине экранирования; такую сферу называют дебаевской. Ее объем

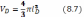
В первом приближении можно считать, что потенциал частицы сказывается только внутри дебаевской сферы, а вне ее пренебрежимо мал. Сопоставляя формулы (8.6) и (8.7), находим

Если от плотности кулоновской энергии перейти к кулоновской энергии, рассчитанной на одну частицу, то

или, из формулы (8.8),

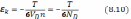
где 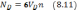— число частиц в дебаевской сфере. В силу статистического характера теории Дебая она приложима лишь при условии, если в дебаевской сфере содержится много частиц

Но тогда, согласно формуле (8.10), кулоновская энергия мала в сравнении с тепловой. Критерием идеальности плазмы может считаться число частиц в дебаевской сфере. Если это число велико, то плазма в термодинамическом отношении ведет себя как идеальный газ. Таким образом, теория Дебая применима только тогда, когда электростатическое взаимодействие является малой поправкой, т. е. когда плазма по своему термодинамическому поведению близка к идеальному газу. Основная ценность приведенных формул в том, что они позволяют проверить, до каких плотностей плазма мало отступает от идеальных газовых законов. В области более высоких плотностей, где эти отступления становятся значительными, теоретический расчет термодинамического поведения плазмы не представляется возможным. Здесь необходимо основываться на экспериментальных данных.