4.5. Электрический дрейф

Оба вида дрейфа в неодно­родном магнитном поле зависят от знака частиц. От них отличается в этом отношении электрический дрейф, т. е. дрейф ча­стиц в магнитном поле при на­личии электрического. Скорость электрического дрейфа

(6.47)

Действительно, электрический заряд в формулу не входит, а с ним исключается зависимость скорости от знака частиц. Электрический дрейф для ионов и для электронов происходит в одну сторону и с одинаковой скоростью, несмотря на большое различие в их массах.

Следует иметь в виду, что формула (6.47) примени­ма только при Е₀<<Н₀, иначе скорость дрейфа получается соизмеримой со скоростью света. Весь же наш вы­вод для дрейфовых скоростей сделан исходя из по­стоянства массы частиц, т. е. для нерелятивистских ско­ростей.

Формулу (6.47) мы получили, подставив в общее вы­ражение (6.43) для скорости дрейфов в магнитном поле значение электрической силы

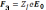(6.48)

Однако ее можно вывести несколько иначе — из об­щего уравнения (6.1). Это целесообразно, если учитывать некоторые полученные полезные физические вы­воды.

Преобразуем уравнение (6.1) в систему отсчета, ко­торая движется относительно исходной (лабораторной) системы координат с постоянной скоростью u'_Д. Ско­рость частицы в движущейся системе u', имлульср'. Скорость в лабораторной системе координат

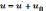(6.49)

Импульс

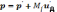(6.50)

Найдем изменение импульса р:

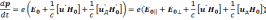(6.51)

где Е_0||и Е_0⊥,—слагающие электрического поля вдоль и перпендикулярно магнитному полю.

Величинуu'_Д можно выбрать таким образом, чтобы выполнялись два условия:

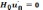(6.52)

и

(6.53)

Условия (6.52) и (6.53) определяют u'_Дсовершенно однозначно. Из условия (6.52) сразу же следует, чтоu'_Д⊥Н₀. Умножим второе условие (6.53) векторно наН_о:

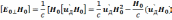(6.54)

Член H₀/c·(u'_ДН₀₎=0 согласно условию (6.52). Следовательно,

(6.55)

т.е. представляет собой дрейфовую скорость. Уравнение движения (6.51) при учете (6.53) запишем

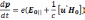(6.56)

Из него полностью выпала компонента E_0пер. Отсюда можно сделать вывод, что влияние E_0пер сводится к созданию дрейфа в направлении, перпендикулярном к магнитному полю. Таким образом, получаем равномерно ускоренное движение вдоль поля и дрейфовое поперек него. Оба движения складываются в движение по па­раболе (рис. 8)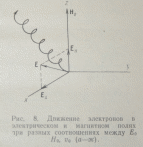 . Если Е₀ лежит в плоскости уz, то и ведущий центр не выйдет из этой плоскости. Поскольку выбор осей х и у произволен, случай, показанный на рис. 8, можно считать довольно общим.

4.6. Дрейф в скрещенных полях

Частным случаем электрического дрейфа является движение в скрещенных электрическом н магнитном полях (E_o┴H_o и u_0пр=0), где u_0пр — начальная скорость частицы вдоль направленияН_о. Ускорение в направлении Н₀ отсутствует. Частица движется по циклоиде, нормальной или укороченной, в зависимости от соотно­шения между угловой скоростью ω_j и скоростью движения центра самой окружности. Последняя зависит от E₀ и начальной скорости u₀=u_0пер вдоль оси у.

Р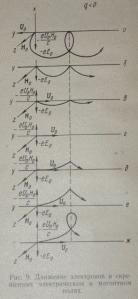 азберем подробнее характер движения в скрещенных полях, поскольку этот случай имеет практическое назначение, особенно для плазменных ускорителей. Рассмотрим движение электрона, а затем определим, в чем состоит отличие для ионов. Нарис. 9, а показано, что происходит, если начальная скорость u₀>0. В этом слу­чае возникает лоренцева сила

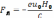(6.57)

направленная антипараллельно оси х. К электрической силе —еЕ₀ добавляется магнитная F_л. Они ускоряют ча­стицу совместно. За ларморовский период τ_е она долж­на пройти большее расстояние, чем при действии только одной —еЕ₀. Это воздействие на частицу определяет движение ее по удлиненной циклоиде.

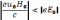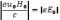На рис. 9,б приведен случай, соответствующий на­чальной скорости u₀=0. При этом получается нормаль­ная циклоида. Далее, если u0<0и , циклоида становится укороченной (рис. 9, в). При уравновешивании обеих сил траектория остается прямолинейной (рис. 9, г). При дальнейшем увеличении u₀ траектория переходит на правую сторону оси х, причем повторяются в обратном порядке те же формы циклоид — укороченная, нормальная и удлинен­ная (рис.9,д — ж). Расстояние между последователь­ными вершинами циклоид

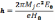(6.58)

Это расстояние не зависит от величины первоначальной скорости u₀.

Для ионов дрейф осуществляется в том же направ­лении, однако вращение происходит в противоположную сторону (рис. 10—сплошные линии). Нетрудно видеть, что дрейф в скрещенных полях происходит по эквипо­тенциальным поверхностям электрического поля, поскольку он направлен по нормали к электрическому полю.