4.4. Дрейфы в магнитных полях

Уравнение движения (6.1) можно решить точно толь­ко в простых случаях, аналогичных уже рассмотренных. При наличии магнитного поля, постоянного во времени и однородного в пространстве, и отсутствии электриче­ских и других сил имеет место движение, которое сла­гается из двух движений — поступательного вдоль по­ля и вращательного в поперечной плоскости. Если маг­нитное поле неоднородно, или на частицу кроме него действуют еще какие-то силы, то такого движения мы уже не получим. Однако в некоторых случаях с извест­ным приближением можно свести реальное движение к вращению частицы по ларморовской окружности, центр которой (так называемый ведущий центр) пере­мещается поперек магнитного поля.

Движение ведущего центра поперек поля называют дрейфом в магнитном поле. Кроме того, при наличии компоненты скорости вдоль направления магнитного поля происходит смещение центра и в этом направле­нии. Такое рассмотрение можно проводить только в случае, когда влияние различных сил проявляется слабо в течение периода обращения частицы в магнитном поле, т. е., иначе говоря, когда выполняются условия адиабатичности (6.27) и (6.34). В этом случае ведущий центр заряженной частицы с магнитным моментом μ_j движется как некая частица в поле силой F с кинетиче­ской энергией W_пер[см. формулу (6.26)].

Приближенная теория движения частиц в адиабати­ческих системах называется дрейфовым приближением, а уравнения, описывающие усредненное движение веду­щего центра и изменение ларморовского радиуса, — дрейфовыми уравнениями. Строгий вывод их довольно сложен. По существу он сводится к рассмотре­нию условий, при которых движение мало отличается от движения в постоянных полях. Действующие силы не должны сильно меняться на протяжении ларморов­ского радиуса, в частности, поперечная сила F_пер не должна приводить к чрезмерному росту поперечных ско­ростей частицы и ларморовского радиуса, что нарушило бы условия адиабатичности. Не может быть большой и продольная сила F_пр. Кроме того, при рассмотрении процессов в плазме, когда применимо дрейфовое при­ближение, не учитывают влияния движения самих частиц на поля, в которых они перемещаются.

Рассмотрим сначала дрейфы в постоянных во време­ни полях. Уравнение (6.1) в проекциях на оси декарто­вых координат:

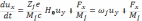
(6.38)

Эту систему можно записать в комплексном виде

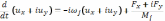(6.39)

Решение неоднородного уравнения (6.39) состоит из общего решения однородного уравнения

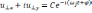(6.40),

котороесоответствует циклотронному вращению, и частного решения

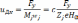(6.41)

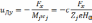(6.42)

В векторном виде

(6.43)

Это и есть скорость дрейфового движения, происхож­дение которого можно наглядно пояснить следующим образом: сила в течение одной половины периода цикло­тронного вращения действует вдоль направления дви­жения частицы, скорость ее возрастает и она должна пройти больший путь, чем за вторую половину периода, когда сила действует против движения.

Как уже было сказано, дрейфовое уравнение (6.43) описывает усредненное движение ведущего центра приблизительно с постоянной скоростью. Быстрое ос­циллирующее движение по ларморовской окружности при этом не принимается в расчет. Следует отметить, что дрейфовое движение (перемещение осциллирующего центра) на первый взгляд обладает рядом свойств, как бы нарушающих привычные представления о законах механики. Действительно, постоянная сила в данном случае вызывает не равномерно ускоренное, а равно­мерное движение. В дальнейшем увидим, что электри­ческое поле не разделяет заряды, а заставляет их дви­гаться в одном направлении, в то время как силы не­электрического происхождения создают электрические токи. Дело в том, что истинным движением все же яв­ляется движение по ларморовской окружности, которое связано с отбором (и отдачей) энергии и подчиняется обычным законам механики.

Дрейфовое же движение представляет собой усред­ненное движение, как следствие циклотронного враще­ния в магнитных полях.