4.1. Движение отдельных заряженных частиц и их потоков

Сначала рассмотрим наиболее простой случай дви­жения отдельных заряженных частиц. С известным при­ближением это рассмотрение применимо к потокам ча­стиц, когда плотности их настолько малы, что всяким взаимодействием между частицами можно пренебречь. Например, для слабых пучков электронов или ионов в вакууме можно не принимать во внимание действие их собственного объемного заряда.

Движение отдельной заряженной частицы описывает­ся следующим общим уравнением:

(6.1)

где М_j— масса частицы (электрона или иона); Z_j— зарядовое число (для электронаZ_e=—1); 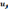— скорость частицы; Н_о— напряженность магнитного по­ля; с—скорость электромагнитных волн в вакууме; F— равнодействующая всех энергетических сил, воз­действующих на частицы (электрических, гравитацион­ных и т. п.).

Воздействие магнитного поля учитывается для удоб­ства отдельно от остальных сил, поскольку оно, дейст­вуя перпендикулярно направлению движения, не изме­няет энергии частиц.

Уравнение (6.1) можно решить лишь в некоторых простейших случаях. Рассмотрим некоторые из них, а затем перейдем к так называемому дрейфовому приближению.

4.2. Движение частиц в электрическом полеE0

В данном случае уравнение (6.1) запишем

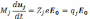(6.2)

где q_j— заряд частицы.

В зависимости от вида поля, т. е. в зависимости его от координат и времени, интегрирование (6.2) дает различные результаты. Рассмотрим некоторые частные примеры, которые пригодятся нам для дальнейшего изложения.

Пример 1. Пусть напряженность поля постоянна как в пространстве, так и во времени (Е₀=const). Найдем траекторию движения иона, влетевшего в это электрическое поле под некоторым углом θ с начальной скоростью u₀. (рис.1)

Интегрируя (6.2), получаем

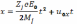(6.3)

(6.4)

где u_0xиu_0y–компоненты начальной скорости. Исключая t, получаем

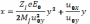(6.5)

Это уравнение параболы. Движение аналогично движению камня, брошенного под углом к горизонту. Это понятно, поскольку электрическое поле и поле тяготения – суть потенциальные.

Пример 2. Электрическое поле однородно в пространстве, но изменяется во времени (для простоты примем гармонический закон изменения E₀). В поле влетает электрон, направление начальной скорости которого перпендикулярно направлению переменного электрического поля. Определим закон движения электрона.

Направим ось у вдоль поля. Тогда

(6.6)

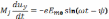(6.7)

Здесь E_m0 – амплитуда напряженности электрического поля; ψ – фазовый угол поля в момент t=0, когда электрон начинает свое движение.

Проинтегрировав (6.6), (6.7), получим

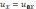(6.8)

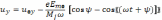(6.9)

где u_0x, u_0y – компоненты начальной скорости электрона. В нашем случае u_0y=0.

Перемещение частицы определяется системой

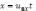(6.10)

(6.11)

Из формул (6.8), (6.9) видно, то происходит стационарный дрейф частиц с постоянной скоростью, на который наложено синусоидальное колебание с амплитудой (рис.2).

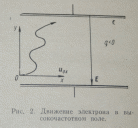Э то происходит, например, в высокочастотных разрядах низкого давления или при очень высоких частотах, когда число упругих соударений электронов с молекулами или ионами ν_m намного меньше, чем частота поля ω. Интересно отметить, что в идеальном приближении (ν_m→0) поглощения высокочастотной энергии не происходит, так как колебательная составляющая скорости сдвинута по фазе с полем на угол π/2, а постоянная в разные полупериоды связана то с поглощением энергии, то с отдачей ее обратно полю.