3 Динамические характеристики

3.1 Динамические характеристики объекта идентификации

Дифференциальное уравнение динамических характеристик объекта идентификации выглядит следующим образом:

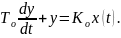
Т_о – оптимальное значение постоянной времени объекта идентификации, К_о – оптимальное значение коэффициента передачи объекта идентификации. Значения были получены в ходе выполнения эксперимента по идентификации объекта регулирования, используем их для построения динамических характеристик.

Переходная функция:

Передаточная функция:

Амплитудно – частотная характеристика:

Фазо – частотная характеристика:

Амлитудно – фазо – частотная характеристика:

Рисунок 14 – Переходная функция объекта идентификации

Рисунок 15 – Амплитудно – частотная характеристика объекта идентификации

Рисунок 16 – Фазо – частотная характеристика объекта идентификации

Рисунок 17 – Вещественная частотная характеристика объекта идентификации

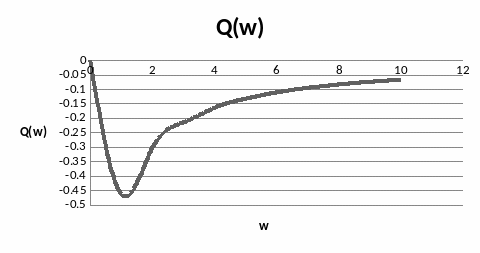
Рисунок 18 – Мнимая частотная характеристика объекта идентификации

Рисунок 19 – Амплитудно – фазо – частотная характеристика объекта идентификации

3.2 Динамические характеристики объекта управления

Переходная функция:

Передаточная функция:

Амплитудно – частотная характеристика:

Фазо – частотная характеристика:

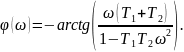
Амплитудно – фазо – частотная характеристика:

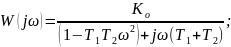
Значения постоянных времени Т₁ и Т₂ находим из выражений:

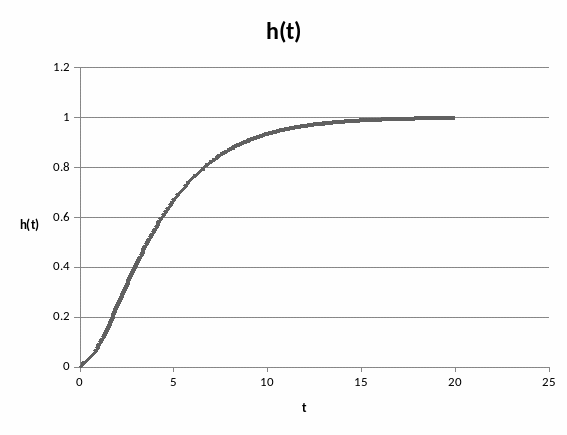Рисунок 20 – Переходная функция объекта управления

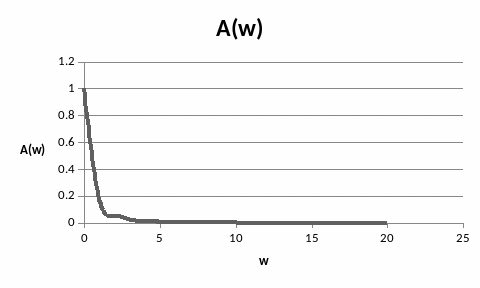
Рисунок 21 – Амплитудно – частотная характеристика объекта управления

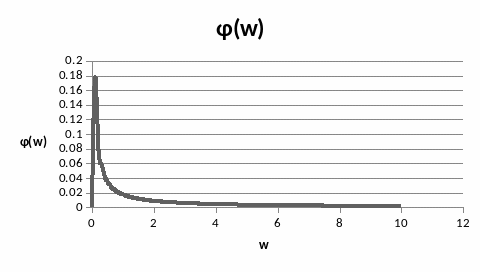
Рисунок 22 – Фазо – частотная характеристика объекта управления

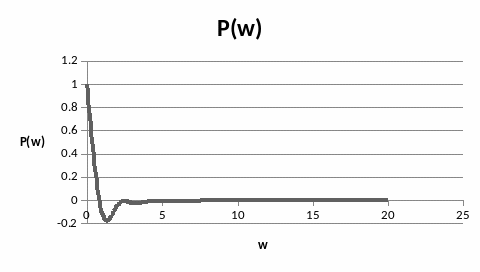
Рисунок 23 – Вещественная частотная характеристика объекта управления

Рисунок 24 – Мнимая частотная характеристика объекта управления

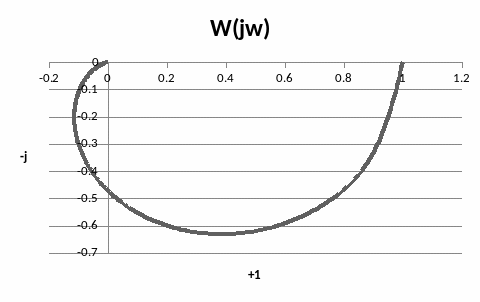
Рисунок 25 – Амплитудно – фазо – частотная характеристика объекта управления

4 Определение спектральной плотности сигнала возмущений

Задача выбора оптимальной системы автоматического регулирования в рамках данной работы рассматривается как задача определения оптимальных параметров регулирующего устройства заданной структуры. Структура изодромного регулятора задана передаточной функцией:

;

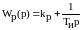где W_p(p) – передаточная функция регулятора; k_p – передаточный коэффициент регулятора; Т_и – время изодрома регулятора.

Объект управления является заданной частью системы и определяется передаточной функцией:

;

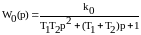Задача выбора оптимальной системы автоматического регулирования в рамках данной работы рассматривается как задача определения оптимальных параметров регулирующего устройства заданной структуры. Структура изодромного регулятора задана передаточной функцией:

;

где Wp(p) – передаточная функция регулятора; k_p – передаточный коэффициент регулятора; Т_и – время изодрома регулятора.

Объект управления является заданной частью системы и определяется передаточной функцией:

.

Расчет спектральной плотности выполняется на ПК по программе «Спектр».

 = 0,2 с; n = 30

Рисунок 26 – Рабочее окно программы «Спектр»

До выполнения программы «Спектр» следует подготовить таблицу ординат автокорреляционной функции R_xx().

Таблица 5 – Правая ветвь автокорреляционной функции входного сигнала

n	Rxx	n	Rxx	n	Rxx
1	352,02	11	30,81	21	-40,92
2	157,36	12	4,03	22	-31,29
3	61	13	-25,12	23	-33,47
4	36,86	14	2,62	24	22,77
5	52,4	15	1,94	25	25,06
6	47,57	16	-22,46	26	-23,35
7	-11,32	17	-49,13	27	-40,59
8	-36,16	18	-46,84	28	-35,82
9	35,35	19	-25,73	29	-19,67
10	65,72	20	-28,04	30	-72,98

Таблица 6 – Спектральная плотность сигнала возмущения

ω	Sx	ω	Sx	ω	Sx
0	85,24	0,75	320,99	1,5	98,58
0,05	88,7	0,8	309,11	1,55	97,41
0,10	98,86	0,85	292,73	1,6	96,58
0,15	115,15	0,9	272,9	1,65	95,54
0,2	136,58	0,95	250,76	1,7	93,92
0,25	161,93	1	227,53	1,75	91,47
0,3	189,73	1,05	204,36	1,8	88,16
0,35	218,38	1,1	182,29	1,85	84,12
0,4	246,28	1,15	162,18	1,9	79,68
0,45	271,89	1,2	144,66	1,95	75,27
0,5	293,85	1,25	130,1	2,	71,43
0,55	311,03	1,3	118,65	2,05	68,74
0,6	322,62	1,35	110,17	2,1	67,76
0,65	328,15	1,4	104,34	2,15	68,95
0,7	327,53	1,45	100,68	2,2	72,67

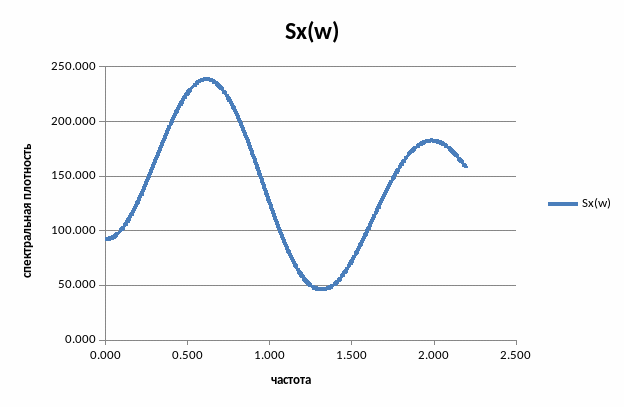
Рисунок 27 – Спектральная плотность сигнала возмущений