Липецкий государственный технический университет

Факультет Автоматизации и Информатики

Кафедра Электрооборудования

КУРСОВАЯ РАБОТА

по теории автоматизации управления

Анализ и синтез оптимальной системы автоматического регулирования

Вариант 30

Студент _________________ Фролов С.Н.

Группа ЭО-14-2

Руководитель

к.т.н, доцент _________________ Шурыгин Ю.А.

Липецк 2016 г.

Задание кафедры

1.1 Формирование типового сигнала возмущающего воздействия на объект в виде реализации случайной функции.

1.2 Выполнение эксперимента по идентификации объекта регулирования. Регистрация реализаций случайной функции на входе и выходе объекта.

1.3 Определение автокорреляционных и взаимокорреляционных функций сигналов, полученных в эксперименте.

1.4 Определение параметров передаточной функции исследуемого объекта методами параметрической идентификации с настраиваемой моделью.

1.5 Определение спектральной плотности сигнала возмущений.

1.6 Поиск оптимальных параметров регулирующего устройства системы авторегулирования по минимуму среднеквадратической ошибки.

1.7 Оценка качества переходной характеристики САР.

Аннотация

С. 40. Ил. 35. Табл. 12. Литература 3 назв.

В представленной курсовой работе при помощи персонального компьютера и программных комплексов «Корреляция», «Идентификация», «Спектр», «Оптимизация» и «Годограф» были произведены анализ и синтез системы автоматического регулирования; найдены параметры объекта идентификации, объекта управления и самой системы автоматического регулирования. Графики зависимостей различных параметров были построены с помощью программы Microsoft Excel.

Оглавление

J = . 29

Q() – мнимая частотная характеристика: 30

A() – амплитудно-частотная характеристика: 30

6 Расчет переходной характеристики САР 36

Библиографический список 40

1 Формирование типового сигнала возмущающего воздействия на объект в виде реализации случайной функции

Реализация случайной величины формируется путём набора ряда случайных чисел. Ряд должен содержать не менее 120 чисел и представ­ляться как в табличной, так и в виде кривой случайной функции. Каждое число должно быть пронумеровано от 1 до 120.

Таблица 1 – Реализация сигнала на входе и выходе объекта исследования

t	x(t)	y(t)	t	x(t)	y(t)	t	x(t)	y(t)	t	x(t)	y(t)
1	57	98	26	17	33	51	18	39	76	45	63
2	56	85	27	28	27	52	16	30	77	73	61
3	79	78	28	12	32	53	47	25	78	86	80
4	61	92	29	47	23	54	51	45	79	76	98
5	68	85	30	66	45	55	53	57	80	53	99
6	84	87	31	65	68	56	49	64	81	50	82
7	40	99	32	45	77	57	32	64	82	34	72
8	61	72	33	33	67	58	49	51	83	60	57
9	45	76	34	63	53	59	21	58	84	45	69
10	36	66	35	50	69	60	19	41	85	60	63
11	59	55	36	33	67	61	9	31	86	72	72
12	61	67	37	44	53	62	40	20	87	53	84
13	41	74	38	67	55	63	26	38	88	37	75
14	42	63	39	85	73	64	62	36	89	56	60
15	28	58	40	75	94	65	79	61	90	64	67

Продолжение таблицы 1.

16	65	46	41	49	96	66	43	85	91	33	76
17	71	68	42	72	78	67	23	69	92	72	57
18	42	81	43	40	87	68	31	47	93	57	78
19	30	66	44	61	67	69	51	43	94	62	76
20	44	51	45	59	74	70	21	56	95	71	78
21	68	54	46	30	76	71	22	40	96	76	86
22	57	73	47	28	55	72	51	33	97	53	94
23	27	74	48	31	44	73	71	52	98	62	80
24	12	52	49	24	42	74	73	75	99	33	80
25	26	32	50	32	36	75	34	86	100	67	59

Данные из таблицы 1 используются для расчета автокорреляционной и взаимокорреляционной функции. Расчет выполняется с применением ПК и программы «Корреляция».

Рисунок 1 – Дисплейное окно программы «Корреляция»

1.1 Выполнение эксперимента по идентификации объекта регулирования

Программа «Корреляция» предназначена для оценки авто - и взаи­мокорреляционных функций реализаций случайных сигналов, полученных в эксперименте. По запросу программы с клавиатуры производится ввод численных значений ста ординат случайной функции на входе объекта x(1), x(2)… x(100) и ста ординат случайной функции на выходе объекта y(1), y(2)… y(100). Программа обеспечивает центрирование случайных функций, расчет и вывод центрированных авто - и взаимокорреляционных функций.

Рисунок 2 – Ввод численных значений ста ординат случайной функции на входе объекта и ста ординат случайной функции на выходе объекта

Вычисление оценок корреляционных функций производится по фор­мулам:

где n − количество дискретных значений случайных функций; m − дискретный аргумент корреляционной функции;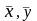 − оценки математиче­ского ожидания сигналов на входе и выходе объекта.

Вычисления проводятся до значения m = (0,05 … 0,1)n. Расчет R_xy производится как для положительных (правая ветвь), так и для отрицатель­ных (левая ветвь) значений m.

1.2 Определение автокорреляционных и взаимокорреляционных функций сигналов

При выполнении расчета по запросу программы вводится требуе­мый интервал сдвига m для автокорреляционной функции, отдельно для правой и для левой ветвей взаимной корреляционной функции. Резуль­таты расчета (ординаты корреляционных функций) в табличной и графи­ческой форме выводятся на экран дисплея и на печать.

Рисунок 3 – Результат расчета

Получившиеся значения R_xy производится как для положительных (правая ветвь), так и для отрицательных (левая ветвь), а также значения R_xx экспортируем в MS Word и MS Excel.

Рисунок 4 – Экспорт данных в MS Word и MS Excel

Таблица 2 – Автокорреляционная и взаимокорреляционная функции

К	Rxx	RxyL	RxyR
0	352,02	147,3	147,3
1	157,36	74,84	321,36
2	61	61,88	260,52
3	36,86	61,67	159,83
4	52,4	40,63	98,41
5	47,57	0,97	76,99
6	−11,32	−3,11	64,32
7	−36,16	56,91	20,51
8	35,35	56,58	−18,69
9	65,72	22,32	13,26
10	30,81	2,54	54,72
11	4,03	−12,63	47,54
12	−25,12	−4,16	28,02
13	2,62	−18,75	−4,29
14	1,94	−43,85	2,02
15	−22,46	−46,34	−0,19

Рисунок 5 – Автокорреляционная Rxx(m) и взаимокорреляционная Rxy(m) функции