
Лекции / Чернова Н.И. Лекции по математической статистике
.pdf

|
|
Упражнение. Доказать свойство K1(б): для любой альтернативы к основной гипо- |
||||||
|
|
тезе (т. е. как только a1 6= a2) величина |ρ| неограниченно возрастает по вероятности |
||||||
|
|
с ростом n и m. |
|
|
|
|
|
|
Оглавление |
Указание. |
Воспользовавшись ЗБЧ или свойствами 2–4 из 1-й лекции, доказать, что |
||||||
|
|
числитель и знаменатель сходятся к постоянным: |
|
|
||||
|
|
|
p |
|
(n − 1)S2 |
(X) + (m − 1)S2(Y) |
p |
|
|
|
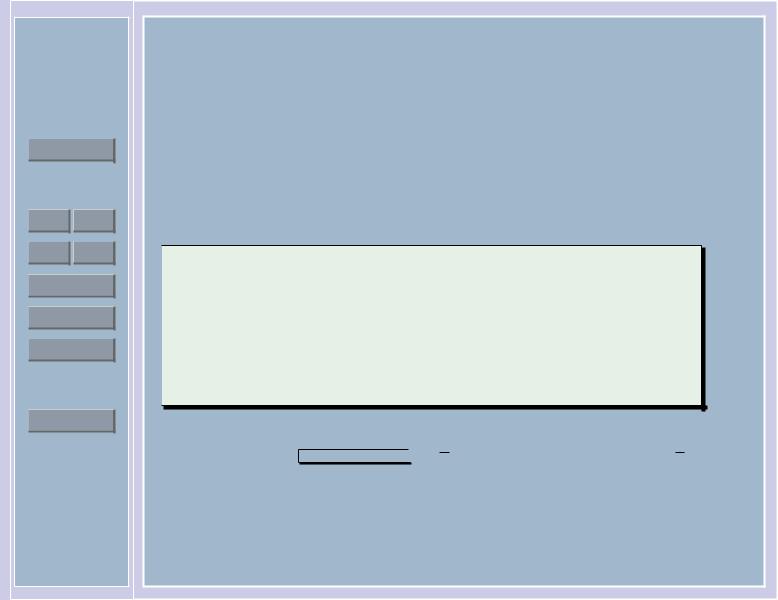
X − Y − |
const 6= 0, |
0 |
0 |
− |
const 6= 0, |
|
JJ |
II |
|
n + m − 2 |
|||||
тогда как |
корень перед дробью неограниченно возрастает. |
→ |
|
|||||
|
|
→ |
|
|
|
|
||
J |
I |
На стр. ... из 180 |
Поэтому остается по ε найти C = τ1−ε/2 — квантиль распределения Tn+m−2. Для |
||||||
|
такого C величина tn+m−2 из распределения Tn+m−2 удовлетворяет равенству |
||||||
Назад |
|||||||
|
|
|
|
|
|
||
|
P (|tn+m−2| > C) = 2P (tn+m−2 > C) = ε. |
||||||
|
|||||||
Во весь экран |
|||||||
|
И критерий Стьюдента выглядит как все критерии согласия: |
||||||
|
|||||||
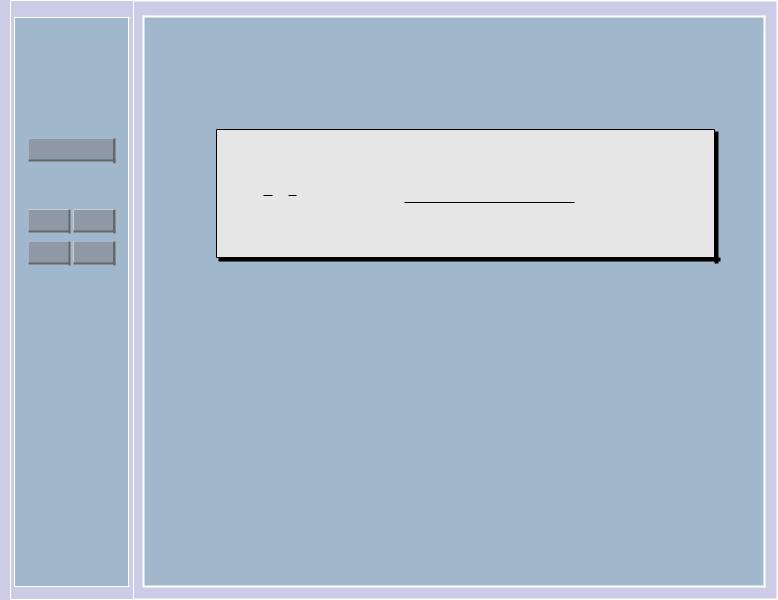
|
H1 |
, |
если ρ(X, Y) |
|
< C, |
||
Уйти |
δ(X, Y) = H2 |
, |
если |ρ(X, Y)| |
> |
C. |
||
|
|
|
| |
| |
|
||
|
Упражнение. Доказать, что этот критерий имеет точный размер ε. |
||||||
Упражнение. Построить критерий для проверки гипотезы о равенстве средних
Стр. 154
двух независимых нормальных выборок с произвольными известными дисперсиями.







 что X − a
что X − a