
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования «Челябинский государственный университет»
Кафедра математики, экономики и управления
Учебная практика отчет
Выполнил студент группы ТПМ-101
Афанасьев Иван Дмитриевич
_________________________________
Подпись
Направление подготовки: 01. 03. 02 - Руководитель: канд. физ. - мат.
Прикладная математика и информатика наук, доцент
Кутузов Антон Сергеевич
Дата защиты 14.07.2017
Оценка____________
Троицк 2017
Содержание
1. СПЕЦИФИКАЦИЯ 2
2. ПРОЕКТИРОВАНИЕ 4
2.1. Модульная структура 4
3. КОДИРОВАНИЕ 5
3.1. Структура текста программы 5
4. ТЕСТИРОВАНИЕ 14
Заключение 17
Литература 17
Спецификация
Дискретное преобразование Фурье (ДПФ, в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье [1].
Быстрое
преобразование Фурье (БПФ, FFT) — алгоритм
быстрого вычисления дискретного
преобразования Фурье (ДПФ). То есть,
алгоритм вычисления за количество
действий, меньшее чем
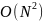 требуемых для прямого (по формуле)
вычисления ДПФ. Иногда под БПФ понимается
один из быстрых алгоритмов, называемый
алгоритмом прореживания по частоте/времени,
имеющий сложность
требуемых для прямого (по формуле)
вычисления ДПФ. Иногда под БПФ понимается
один из быстрых алгоритмов, называемый
алгоритмом прореживания по частоте/времени,
имеющий сложность
 [1].
[1].
Дискретное
преобразование Фурье преобразует набор
чисел
 в
набор чисел
в
набор чисел
 ,
такой, что
,
такой, что
 ,
где
,
где
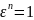 и
и
 при
при
 [1].
[1].
Особенность
БПФ заключается в том, что алгоритм
расчета происходит с помощью рекурсивной
функции, которая и позволяет уменьшить
сложность расчёта до
,
кроме того, для реализации алгоритма
требуется количество элементов, равное
степени двойки. Чаще всего этот алгоритм
применяют в поле комплексных чисел (при
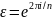 ).
).
Описание входных данных: список комплексных чисел
Описание выходных данных: преобразованный список комплексных чисел, выходные данные записываются в файл testfile.txt
Для контроля правильности применяем обратное преобразование
Таблица 1. Примеры входных и выходных данных
Входные данные |
Выходные данные |
[(1+1j),(1+1j),(1+1j),(1+1j)] |
[(4+4j),(0+0j),(0+0j),(0+0j)] |
[(3+1j),(15-4j),(-5+2j),(2-2j),(-1-4j)] |
Вывод окна ошибки, оповещающее, что количество введенных чисел должно соответствовать степени двойки |
[(1+0j),(2+0j),(3+0j),(4+0j),1j,2j,3j,4j] |
[(10+10j),(6.8284+7.6568j),(0-4j) (3.6569-1.1716j),(-2-2j),(1.1716-3.6569j) (-4+0j),(-7.6569-6.8284j)] |
