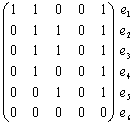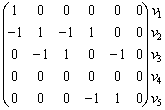Описание[править | править вики-текст]

При помощи четырех бит можно закодировать шестнадцать цифр. Из них используются 10. Остальные 6 комбинаций в двоично-десятичном коде являются запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр:

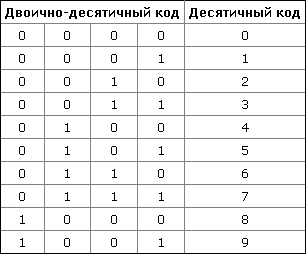
Двоично-десятичный код также применяется в телефонной связи. В этом случае кроме десятичных цифр кодируются символы '*' или '#' или любые другие. Для записи этих символов в двоично-десятичном коде используются запрещенные комбинации:

Преимущества и недостатки[править | править вики-текст] Преимущества[править | править вики-текст]

Часы с двоично-десятичной системой индикации. В этих часах каждая колонка отображает десятичное число в двоично-десятичной системе.

• Упрощён вывод чисел на индикацию — вместо последовательного деления на 10 требуется просто вывести на индикацию каждый полубайт. Аналогично, проще ввод данных с цифровой клавиатуры.

• Для дробных чисел (как с фиксированной, так и с плавающей запятой) при переводе в человекочитаемый десятичный формат и наоборот не теряется точность.

• Упрощены умножение и деление на 10, а также округление.

По этим причинам двоично-десятичный формат применяется в калькуляторах — калькулятор в простейших арифметических операциях должен выводить в точности такой же результат, какой подсчитает человек на бумаге.

Недостатки[править | править вики-текст]

• Требует больше памяти.

• Усложнены арифметические операции. Так как в 8421-BCD используются только 10 возможных комбинаций 4-х битового поля вместо 16, существуют запрещённые комбинации битов: 1010(10₁₀), 1011(11₁₀), 1100(12₁₀), 1101(13₁₀), 1110(14₁₀) и 1111(15₁₀).

Поэтому, при сложении и вычитании чисел формата 8421-BCD действуют следующие правила:

1. При сложении двоично-десятичных чисел каждый раз, когда происходит перенос бита в старший полубайт, необходимо к полубайту, от которого произошёл перенос, добавить корректирующее значение 0110 (= 6₁₀ = 16₁₀ — 10₁₀: разница количеств комбинаций полубайта и используемых значений).

2. При сложении двоично-десятичных чисел каждый раз, когда встречается недопустимая для полубайта комбинация, необходимо к каждой недопустимой комбинации добавить корректирующее значение 0110 с разрешением переноса в старшие полубайты.

3. При вычитании двоично-десятичных чисел, для каждого полубайта, получившего заём из старшего полубайта, необходимо провести коррекцию, отняв значение 0110.

Сложение нормализованных чисел

Сложение и вычитание

При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.

В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.

В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.

Пример 1. Сложить двоичные нормализованные числа 0.10111 . 2–1 и 0.11011 . 210. Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:

Сложение в двоично-десятичной форме

Суть двоично-десятичных двоичных чисел заключается в том, что на запись каждой цифры отводится 4 младших бита, а 4 старших бита отводятся под запись ANSII кода. Например, десятичное число 31110 будет записано в двоичной системе счисления в двоичном коде как 111100110000110, а в двоично-десятичном коде как 00000011 00000001 00000001 00000001 00000000, то есть на каждое число отводится по 4 младших бита, либо в формате ANSII 00110011 00110001 00110001 00110001 00110000 значения величин в формате слова и двойного слова имеют ограниченный диапазон. Если программа предназначена для работы в области финансов, то ограничение суммы в рублях величиной 65 536 (для слова) или даже 4 294 967 296 (для двойного слова) будет существенно сужать сферу ее применения, данную проблему решают подобные числа, они не ограничивают размер данных, хотя и приходится тратить больше памяти на хранение чисел

Преимущества

• Упрощён вывод чисел на индикацию — вместо последовательного деления на 10 требуется просто вывести на индикацию каждый полубайт. Аналогично, проще ввод данных с цифровой клавиатуры.

• Для дробных чисел (как с фиксированной, так и с плавающей запятой) при переводе в человекочитаемый десятичный формат и наоборот не теряется точность.

• Упрощены умножение и деление на 10, а также округление. По этим причинам двоично-десятичный формат применяется в калькуляторах — калькулятор в простейших арифметических операциях должен выводить в точности такой же результат, какой подсчитает человек на бумаге.

Недостатки

• Усложнены арифметические операции.

• Требует больше памяти.

• В двоично-десятичном коде 8421-BCD существуют запрещённые комбинации битов: Запрещённые в 8421-BCD битовые комбинации

1010 1011 1100

1101 1110 1111

Характеристика канала связи

Ширина полосы пропускания - полоса частот, в пределах которой неравномерность частотной характеристики не превышает заданной.

Ширина полосы обычно определяется как разность верхней и нижней граничных частот участка АЧХ  , на которомамплитуда колебаний равняется   (или, что эквивалентно   для мощности) от максимальной. Этот уровень приблизительно соответствует −3 дБ.

Иногда полосу пропускания определяют также по фазо-частотной характеристике устройства^[1].

Ширина полосы пропускания выражается в единицах частоты (например, в герцах).

В радиосвязи и устройствах передачи информации расширение полосы пропускания позволяет передать большее количество информации.

Пропускная способность канала

Наибольшая возможная в данном канале скорость передачи информации называется его пропускной способностью. Пропускная способность канала есть скорость передачи информации при использовании «наилучших» (оптимальных) для данного канала источника, кодера и декодера, поэтому она характеризует только канал.

Номинальная скорость — битовая скорость передачи данных без различия служебных и пользовательских данных. Эффективная скорость — скорость передачи пользовательских данных (нагрузки). Этот параметр зависит от соотношения накладных расходов и полезных данных.

Пропускная способность дискретного (цифрового) канала без помех

C = log m × Vт,

где m — основание кода сигнала, используемого в канале. Скорость передачи информации в дискретном канале без шумов (идеальном канале) равна его пропускной способности, когда символы в канале независимы, а все m символов алфавита равновероятны (используются одинаково часто). Vт - символьная скорость передачи.

Скорость передачи данных — объём данных, передаваемых за единицу времени^[1]. Максимальная скорость передачи данных без появления ошибок (пропускная способность) вместе с задержкой^[en] определяют производительность системы или линии связи. Теоретическая верхняя граница скорости передачи определяется теоремой Шеннона — Хартли.

Рассматривая все возможные многоуровневые и многофазные методы шифрования, теорема Шеннона — Хартли утверждает, что ёмкость канала C, означающая теоретическую верхнюю границу скорости передачи информации, которые можно передать с данной средней мощностью сигнала S через один аналоговый канал связи, подверженный аддитивному белому гауссовскому шуму мощности N равна:

где

C — ёмкость канала в битах в секунду;

B — полоса пропускания канала в герцах;

S — полная мощность сигнала над полосой пропускания, измеренной в ваттах или вольтах в квадрате;

N — полная шумовая мощность над полосой пропускания, измеренной в ваттах или вольтах в квадрате;

S/N — отношение сигнала к гауссовскому шуму, выраженное как отношение мощностей.

Бит четности

В вычислительной технике и сетях передачи данных би́том чётности (англ. Parity bit) называют контрольный бит, служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе).

В последовательной передаче данных часто используется формат 7 бит данных, бит чётности, один или два стоповых бита. Такой формат аккуратно размещает все 7-битные ASCII символы в удобный 8-битный байт. Также допустимы другие форматы: 8 бит данных и бит чётности.

В последовательных коммуникациях чётность обычно контролируется оборудованием интерфейса (например UART). Признак ошибки становится доступен процессору (и ОС) через статусный регистр оборудования. Восстановление ошибок обычно производится повторной передачей данных, подробности которого обрабатываются программным обеспечением (например, функциями ввода-вывода операционной системы)

Контроль некой двоичной последовательности (например, машинного слова) с помощью бита чётности также называют контролем по паритету. Контроль по паритету представляет собой наиболее простой и наименее мощный метод контроля данных. С его помощью можно обнаружить только одиночные ошибки в проверяемых данных. Двойная ошибка будет неверно принята за корректные данные. Поэтому контроль по паритету применяется к небольшим порциям данных, как правило к каждому байту, что даёт коэффициент избыточности для этого метода 1/8. Метод редко применяется в компьютерных сетях из-за невысоких диагностических способностей. Существует модификация этого метода — вертикальный и горизонтальный контроль по паритету. Отличие состоит в том, что исходные данные рассматриваются в виде матрицы, строки которой составляют байты данных. Контрольный разряд подсчитывается отдельно для каждой строки и для каждого столбца матрицы. Этот метод обнаруживает значительную часть двойных ошибок, однако обладает большей избыточностью. Он сейчас также почти не применяется при передаче информации по сети.

Расстояние по Хемменгу

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух слов одинаковой длины различны^[1]. В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых q-ичных алфавитов и служит метрикой различия (функцией, определяющей расстояние в метрическом пространстве) объектов одинаковой размерности.

Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей, в этом случае расстоянием Хэмминга   между двумя двоичными последовательностями (векторами)   и   длины   называется число позиций, в которых они различны — в такой формулировке расстояние Хэмминга вошло в словарь алгоритмов и структур данных национального института стандартов и технологий США (англ. NIST Dictionary of Algorithms and Data Structures). Расстояние Хэмминга является частным случаем метрики Минковского (при соответствующем определении вычитания):

.

Коды, исправляющие ошибки

Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.

Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.

С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.

В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).

По способу работы с данными коды, исправляющие ошибки, делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.

Классификация данных. Представление элементарных данных в ОЗУ.

Как уже сказано, различными типами элементарных данных являются символы, целые числа, вещественные числа и логические данные. Логический и физический уровни их представления определяются конструктивными особенностями ОЗУ компьютера. В частности, поскольку память компьютера имеет байтовую структуру, к ней привязывается представление любых данных. Более точным является утверждение, что для представления значений элементарных данных в памяти компьютера используется машинное слово; этот термин в информатике применяется в двух значениях:

Машинное слово - (1) совокупность двоичных элементов, обрабатываемая как единое целое в устройствах и памяти компьютера;

(2) данные, содержащиеся в одной ячейке памяти компьютера.

С технической точки зрения машинное слово объединяет запоминающие элементы, служащие для записи 1 бит информации, в единую ячейку памяти. Количество таких объединяемых элементов кратно 8, т.е. целому числу байт. Например, в отечественной ЭВМ БЭСМ-6 длина машинного слова составляла 48 бит (6 байт), в машинах СМ и IBM - 16 бит (2 байта). Доступ к машинному слову в операциях записи и считывания осуществляется по номеру ячейки памяти, который называется адресом ячейки.

Запоминающие устройства, в которых доступ к данным осуществляется по адресу ячейки, где они хранятся, называются устройствами с произвольным доступом.*

* Именно по этой причине в англоязычной литературе вместо ОЗУ используется термин RAM – Random Access Memory - «память с произвольной выборкой».

Время поиска нужной ячейки, а также продолжительность операций считывания или записи в ЗУ произвольного доступа одинаково для всех ячеек независимо от их адреса.

Для логического уровня важно то, что представление значений любых элементарных данных должно быть ориентировано на использование машинных слов определеннойи единой для данного компьютера длины, поскольку их представление на физическом уровне производится именно в ячейках ОЗУ (на ВЗУ элементарные данные в качестве самостоятельных не представляются и доступ к ним отсутствует).

Рассмотрим особенности представления всех типов элементарных данных с помощью 16-битного машинного слова. Порядок размещения значений данных представлен на рис.6.1.

Для представления символов (литерных данных) машинное слово делится на группы по 8 бит, в которые и записываются двоичные коды символов. Ясно, что в 16-битном машинном слове могут быть записаны одновременно два символа (рис. 6.1,а). Значениями одиночных литерных данных являются коды символов. Множество допустимых значений данных этого типа для всех кодировок, основанных на однобайтовом представлении, составляет 2⁸ - 256; двубайтовая кодировка Unicode допускает 65536 значений. Совокупность символов образует алфавит, т.е. для них установлен лексикографический порядок следования в соответствии с числовым значением кода; это, в свою очередь, позволяет определить над множеством символьных данных операции математических отношений >, <, =. Непосредственно над одиночной символьной переменной определена единственная операция - изменение значения с одного кода на другой. Все остальные действия производятся со сложными символьными данными, например, типа String в языке PASCAL (см. п.6.3.).

В представлении целых чисел со знаком (например, тип Integer в языке PASCAL) старший бит (15-й), как уже обсуждалось ранее, отводится под запись знака числа (0 соответствует «+», 1 - «-»), а остальные 15 двоичных разрядов - под запись прямого (для положительного) или обратного (для отрицательного) двоичного кода числа (рис. 6.1,6). При этом возможные значения чисел ограничены интервалом [-32768 + 32767]. Наряду с описанным используется и другой формат представления целых чисел -беззнаковый; очевидно, он применим только для записи положительных чисел. В этом случае под запись числа отводятся все 16 двоичных разрядов, и интервал разрешенных значений оказывается [0 * 65535] (в PASCAL'e такой числовой тип называется Word). Помимо математических отношений над целыми числами определены операции сложения, вычитания и умножения (в тех случаях, когда они не приводят к переполнению разрядной сетки), а также целочисленного деления и нахождения остатка от целочисленного деления.

Представление вещественных чисел с плавающей запятой также рассматривалось ранее. При записи числа оно переводится в нормализованную форму с выделением и отдельным хранением знака мантиссы, знака порядка, порядка и мантиссы. Для представления числа отводится несколько машинных слов. Ситуация, соответствующая числовому типу Single в языке PASCAL, когда для представления числа отводится два машинных слова, проиллюстрирована на рис. 6.1,в. Этой формой охватывается диапазон модулей мантиссы [1,5∙10^-45¸3,4∙10³⁸] с 7-ю десятичными цифрами мантиссы. Запись мантиссы начинается с 23-го разряда. Поскольку мантисса выбирается такой, чтобы ее модуль отвечал условию 0,1₂ ≤ |M₂| < 1, всегда значение старшего разряда числа 0 (целых) - оно не отображается при записи, а значение следующего разряда всегда 1. В процессе выполнения операций может произойти переполнение разрядной сетки (на 1 разряд) или, наоборот, ее освобождение (т.е. в первом отображаемом разряде окажется 0) - по этой причине после каждой операции с числами в такой форме производится нормализация результата, которая состоит в таком изменении порядка числа и сдвиге мантиссы, чтобы первой значащей цифрой снова оказалась 1 (см. п.4.3.3.). Изменение порядка в представлении числа эквивалентно перемещению разделителя целой и дробной частей числа - как уже говорилось, такая форма получила название «с плавающей запятой». Благодаря применению плавающей запятой производится автоматическое масштабирование чисел в ходе вычислений, что снижает погрешность их обработки. Над вещественными числами определены все четыре арифметические операции. Помимо этого имеются операции преобразования вещественного типа к целому (например, round и trunc в PASCAL'e).

Логические данные могут принимать одно из двух значений - 0 или 1 (0 соответствует логическому False, 1 - True, причем, принимается False<True). Для их записи было бы достаточно отвести всего один двоичный разряд. Однако в ОЗУ компьютера отсутствует доступ к отдельному биту, поэтому для представления логических данных выделяется целый байт, в младший разряд которого и помещается значение. Таким образом, в машинном слове логические данные располагаются в 0-м и в 8-м битах (см. рис. 6.1, г). Над логическими данными определены операции: логическое умножение (конъюнкция, ^), логическое сложение (дизъюнкция, v), логическое отрицание (Ø). Примером логических данных может служить тип Boolean в PASCAL'e

Структуры данных и их представление в ОЗУ

Можно указать ряд причин, поясняющих необходимость и удобство использования данных, организованных в некоторую структуру:

· отражение в организации данных логики задачи, объективно существующей взаимосвязи и взаимообусловленности между данными;

· оптимизация последовательности обработки данных;

· широкое применение при обработке данных циклических конструкций - в них при переборе нельзя автоматически менять имя переменной, однако, можно изменять индексы;

· неудобство использования большого количества одиночных данных, поскольку это ведет к необходимости использования многих имен.

Перечисленные причины приводят к тому, что в современных языках и системах программирования резервируется широкий спектр различных структур данных и, помимо этого, предусматривается возможность создания структур удобных и необходимых пользователю.

Относительно структур данных необходимо сделать следующие общие замечания:

· логический уровень организации данных отражается в тексте программы - им определяется порядок обработки данных;

· физический уровень представления структур в ОЗУ имеет всего две разновидности: последовательные списки и связные списки (см. п.6.3.3); на ВЗУ все структуры представляются в виде файлов;

· обработка данных возможна только после их размещения в ОЗУ; с 63У определены только операции записи и чтения;

· идентификаторы, как и у одиночных данных, существуют только в тексте программы и на этапе трансляции переводятся в адреса ячеек памяти.

Массив, стек, список

Массив (в некоторых языках программирования также таблица, ряд, матрица) — набор компонентов (элементов), расположенных в памяти непосредственно друг за другом, доступ к которым осуществляется по индексу (индексам). В отличие от списка, массив является структурой с произвольным доступом^[1].

Размерность массива — количество индексов, необходимое для однозначного доступа к элементу массива^[2][3].

Форма или структура массива — количество размерностей и размер (протяжённость) массива для каждой размерности^[4], может быть представлен одномерным массивом^[5].

В языке программирования APL массив является основным типом данных (при этом нуль-мерный массив называется скаляром, одномерный — вектором, двумерный — матрицей)^[5].

Стек - механизм реализующий правило "первым вошёл - последним вышел". Английская аббревиатура правила: FILO - First In - Last Out. Элементы добавляются и изымаются с вершины стека. Очередь - механизм реализующий правило "первым вошёл - первым вышел". Английская аббревиатура правила: FIFO - First In - First Out. Элементы добавляются в конец очереди, а изымаются - из начала. Связанный список - структура, в которой каждый элемент содержит указатели на другие элементы списка (например, на предыдущий или (и) на следующий элемент в списке).

Особенности устройств, используемых для хранения информации в компьютерах

Не вдаваясь глубоко в техническую сторону, рассмотрим некоторые особенности устройств, используемых для хранения информации в компьютерах.

Устройства, выполняющие операции, связанные с сохранения и считывания данных на материальном носителе, называются внешними запоминающими устройствами(ВЗУ) или устройствами внешней памяти.

Любое ВЗУ реализует один из двух возможных принципов размещения информации - последовательный доступ или прямой доступ. Первый вариант используется при сохранении информации на ленточных носителях, например, магнитной или бумажной ленте - в этом случае записи размещаются одна за другой, т.е. последовательно. Считывание записей также производится последовательно, и для того, чтобы отыскать нужную запись, требует просмотреть все предыдущие, подобно поиску кадра на кинопленке.

Для реализации прямого доступа на носителе должны быть обозначены (пронумерованы) области для записи информации - такие области называются блоками. Блок, подобно ячейке ОЗУ, служит контейнером для размещения данных. Обратиться к данным для записи-считывания можно по номеру (идентификатору) блока. Операция разбиения поверхности носителя на блоки называется форматированием - она производится в обязательном порядке и предшествует использованию носителя. Блок обычно имеет строго определенную для данного носителя информационную емкость, например, для сменного магнитного диска емкостью 1,44 Мб - 512 байт. Блок может содержать только целое число физических записей - из-за этого часть блока длиной меньше, чем размер записи, оказывается пустой и не используется. Например, при длине записей по 150 байт в один блок размером 512 байт поместятся 3 записи, а 62 байта останутся свободными. На носителях большой емкости, например, жестких магнитных дисках (винчестерах) блоки объединяются в группы - кластеры (например, на современных компьютерах IBM кластер охватывает 8 блоков) -запись файлов производится в них и применяется адресация по номерам кластеров (это уменьшает общее количество адресов и, следовательно, ускоряет поиск и доступ к файлу).

На дисковых носителях имена файлов хранятся отдельно от физических записей. В определенном месте диска при его форматировании создается специальная область, в которой располагается таблица размещения файлов - FAT (File Allocation Table). В эту таблицу заносятся имена и атрибуты файлов (дата и время создания, размер, атрибуты доступа), а также номер кластера, с которого начинается размещение файла. Таким образом, обращение к файлу происходит в два этапа: сначала с помощью файловой таблицы по имени файла находится номер кластера, а затем считывающе-записывающая головка ВЗУ устанавливается над ним и производит операции. Ситуация иллюстрируется рис. 6.7. Содержание файловой таблицы можно просмотреть с помощью команд операционной системы (например, dir в MS DOS).

При обмене между ВЗУ и ОЗУ данные пересылаются не отдельными записями, а блоками, размер которых совпадает с размером блока ВЗУ - 512 байт; схема обмена представлена на рис.6.8. Для организации обмена в ОЗУ выделяется специальная область - буфер обмена; размер буфера устанавливается при конфигурировании операционной системы компьютера. При пересылке из ОЗУ в ВЗУ данные (записи, входящие в файл) сначала из ОЗУ пересылаются в буфер, пока он не заполнится, затем целым блоком отправляются в подготовленный блок ВЗУ. Считывание идет обратным путем. Обмен может идти минуя центральный процессор - в этом случае одновременно с обменом может производиться обработка данных (поступивших или иных).

Представление данных на внешних запоминающих устройствах

внешние устройства имеют свою собственную кэш-память. Обмен данными внутри процессора происходит в несколько раз быстрее, чем обмен с другими устройствами, например с оперативной памятью. Для того чтобы уменьшить количество обращений к оперативной памяти, внутри процессора создают бу- ферную область – так называемую кэш-память. Это как бы «сверхоперативная память». Когда процессору нужны данные, он сначала обращается в кэш- память, и только если там нужных данных нет, происходит его обращение в оперативную память. Принимая блок данных из оперативной памяти, процес- сор заносит его одновременно и в кэш-память. «Удачные» обращения в кэш- память называют попаданиями в кэш. Процент попаданий тем выше, чем боль- ше размер кэш-памяти, поэтому высокопроизводительные процессоры ком- плектуют повышенным объемом кэш-памяти. Сегодня кэш-память устанавли- вается «пирамидой».

Единицы представления данных

Существует множество систем представления данных. С одной из них,

принятой в информатике и вычислительной технике, двоичным кодом, мы по-

знакомились выше. Наименьшей единицей такого представления является бит (двоичный разряд). Группы из восьми битов называются байтами. Байт – ми- нимальная адресуемая ячейка памяти.

Группа из 16 взаимосвязанных битов (двух взаимосвязанных байтов) в ин- форматике называется словом. Соответственно, группы из четырех взаимосвя- занных байтов (32 бита) называются удвоенным словом.

Файловые структуры

Вся совокупность файлов на диске и взаимосвязей между ними называется файловой структурой. Различные ОС могут поддерживать разные организации файловых структур. Существуют две разновидности файловых структур: простая, или одноуровневая, и иерархическая - многоуровневая.

Одноуровневая файловая структура - это простая последовательность файлов. Для отыскания файла на диске достаточно указать лишь имя файла. Например, если файл tetris.exe находится на диске А:, то его "полный адрес" выглядит так:

A:\tetris.exe

Операционные системы с одноуровневой файловой структурой используются на простейших учебных компьютерах, оснащенных только гибкими дисками.

Многоуровневая файловая структура - древовидный (иерархический) способ организации файлов на диске. Для облегчения понимания этого вопроса воспользуемся аналогией с традиционным "бумажным" способом хранения информации. В такой аналогии файл представляется как некоторый озаглавленный документ (текст, рисунок) на бумажных листах. Следующий по величине элемент файловой структуры называется каталогом. Продолжая "бумажную" аналогию, каталог будем представлять как папку, в которую можно вложить множество документов, т. е. файлов. Каталог также получает собственное имя (представьте, что оно написано на обложке папки).

Каталог сам может входить в состав другого, внешнего по отношению к нему каталога. Это аналогично тому, как папка вкладывается в другую папку большего размера. Таким образом, каждый каталог может содержать внутри себя множество файлов и вложенных каталогов (их называют подкаталогами). Каталог самого верхнего уровня, который не вложен ни в какой другой каталог, называется корневым каталогом.

В операционной системе Windows для обозначения понятия "каталог" используется термин "папка".

Графическое изображение иерархической файловой структуры называется деревом.

Роль операционной системы

Операционная система — это комплекс взаимосвязанных системных программ, назначение которого — организовать взаимодействие пользователя с компьютером и выполнение всех других программ.

Операционная система выполняет роль связующего звена между аппаратурой компьютера, с одной стороны, и выполняемыми программами, а также пользователем, с другой стороны.

Операционная система обычно хранится во внешней памяти компьютера — на диске. При включении компьютера она считывается с дисковой памяти и размещается в ОЗУ.

Этот процесс называется загрузкой операционной системы.

В функции операционной системы входит:

осуществление диалога с пользователем;

ввод-вывод и управление данными;

планирование и организация процесса обработки программ;

распределение ресурсов (оперативной памяти и кэша, процессора, внешних устройств);

запуск программ на выполнение;

всевозможные вспомогательные операции обслуживания;

передача информации между различными внутренними устройствами;

программная поддержка работы периферийных устройств (дисплея, клавиатуры, дисковых накопителей, принтера и др.).

Операционную систему можно назвать программным продолжением устройства управления компьютера. Операционная система скрывает от пользователя сложные ненужные подробности взаимодействия с аппаратурой, образуя прослойку между ними. В результате этого люди освобождаются от очень трудоёмкой работы по организации взаимодействия с аппаратурой компьютера.

Понятия алгоритма и его свойства

Алгоритм – описание последовательности действий (план), строгое исполнение которых приводит к решению поставленной задачи за конечное число шагов.

Вы постоянно сталкиваетесь с этим понятием в различных сферах деятельности человека (кулинарные книги, инструкции по использованию различных приборов, правила решения математических задач...). Обычно мы выполняем привычные действия не задумываясь, механически. Например, вы хорошо знаете, как открывать ключом дверь. Однако, чтобы научить этому малыша, придется четко разъяснить и сами эти действия и порядок их выполнения: 1. Достать ключ из кармана. 2. Вставить ключ в замочную скважину. 3. Повернуть ключ два раза против часовой стрелки. 4. Вынуть ключ.

Если вы внимательно оглянитесь вокруг, то обнаружите множество алгоритмов которые мы с вами постоянно выполняем. Мир алгоритмов очень разнообразен. Несмотря на это, удается выделить общие свойства, которыми обладает любой алгоритм.

Свойства алгоритмов: 1. Дискретность (алгоритм должен состоять из конкретных действий, следующих в определенном порядке); 2. Детерминированность (любое действие должно быть строго и недвусмысленно определено в каждом случае); 3. Конечность (каждое действие и алгоритм в целом должны иметь возможность завершения); 4. Массовость (один и тот же алгоритм можно использовать с разными исходными данными); 5. Результативность (отсутствие ошибок, алгоритм должен приводить к правильному результату для всех допустимых входных значениях).

Виды алгоритмов: 1. Линейный алгоритм (описание действий, которые выполняются однократно в заданном порядке); 2. Циклический алгоритм (описание действий, которые должны повторятся указанное число раз или пока не выполнено задание); 3. Разветвляющий алгоритм (алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий)  4. Вспомогательный алгоритм (алгоритм, который можно использовать в других алгоритмах, указав только его имя).

Символьная форма представления алгоритма

Символьная запись представляет собой последовательность строк, каждая из которых содержит описание одного или нескольких действий. Для человека символьная алгоритмическая запись может быть приближена к естественному языку. Для технического устройства запись производится на специализированном формализованном языке. Недостатком символьной формы представления алгоритма является невозможность целостного восприятия логической структуры алгоритма.

Виды символьной записи

Пошагово-словеснаяформа представляет собой пронумерованную последовательность строк, каждая из которых содержит описание конкретных действий на естественном языке. Данная форма применяется в том случае, если исполнителем является человек (кулинарные рецепты, представляющие порядок действий; алгоритм Евклида; действия, предлагаемые программной при установке программы; организация справки по какому-либо программному обеспечению и т.д.).

Пример. Алгоритм Евклида нахождения наибольшего общего делителя:

1. Если два числа равны, то наибольший общий делитель – их значение. Идти к пункту 4

2. Большее число заменить на разность большего и меньшего

3. Вернуться к пункту 1

4. Конец алгоритма

Формула – строчная запись действий, обеспечивающих обработку числовых, символьных или логических данных.

Псевдокод –ориентированный на исполнителя «человек» частично формализованный язык, позволяющий записывать алгоритмы в форме, близкой как к языкам программирования, так и к естественному языку.

В псевдокоде строго определены только правила записи управляющих структур, а описание самих действий остается естественным. Псевдокод имеет русскоязычную основу и используется, в основном, при обучении азам программирования. Конструкции псевдокода позволяют легко перейти от словесных алгоритмов к языкам программирования.

Графическая форма представления алгоритма

Графическая форма представления называется блок-схема,в которой для представления отдельных блоков алгоритма используется обусловленный набор геометрических фигур. Графическая форма предназначена только для человека и главное достоинство – наглядность; блок-схема позволяет охватить весь алгоритм сразу, отследить различные варианты его выполнения. По блок-схеме гораздо проще осуществляется запись алгоритма на каком-либо формальном языке. Графическое представление конструкций формального языка (условные операторы, циклические операторы и т.д.) осуществляется посредствам синтаксических диаграмм.

Структурная теорема

После того, как были рассмотрены возможные способы записи алгоритмов, вполне закономерным представляется вопрос о технологии их разработки. До середины 60-х годов теории разработки алгоритмов не существовало - процесс разработки целиком определялся опытом и искусством программиста. Однако по мере роста сложности программ возникла необходимость создания методологии их разработки, и она появилась в виде структурного программирования. Идеи структурного программирования были высказаны в 1965 г. Э. Дейкстрой, но сведены в некую законченную систему правил они не были. В том же году итальянские математики К. Бом и Д. Джакопини сформулировали теорему о структурности. Прежде, чем рассмотреть ее суть, необходимо ввести некоторые понятия.

Поскольку алгоритм определяет порядок обработки информации, он должен содержать, с одной стороны, действия по обработке, а с другой стороны, порядок их следования, называемым потоком управления.

Рассмотренные выше блоки, связанные с обработкой данных, делятся на простые и условные. Особенность простого действия в том, что оно имеет один вход и один выход, в отличии от условного, обладающим двумя выходами в зависимости от того, истинным ли окажется условие. Простое действие не означает, что оно единственное - это может быть некоторая последовательность действий.

Часть алгоритма, организованная как простое действие, т.е. имеющая один вход (выполнение начинается всегда с одного и того же действия) и один выход (т.е. после завершения данного блока всегда начинает выполняться одно и то же действие), называется функциональным блоком.

Из этого определения, в частности, следует, что каждое простое действие является функциональным блоком, а условное - нет.

Согласно положениям структурного программирования можно выделить всего три различных варианта организации потока управления действиями алгоритма. Поток управления может обладать следующими свойствами:

1) каждый блок выполняется не более одного раза;

2) выполняется каждый блок.

Поток управления, в котором выполняются оба эти свойства, называется линейным - в нем несколько функциональных блоков выполняются последовательно. Линейному потоку на языке блок-схем соответствует структура:

Очевидно несколько блоков, связанных линейным потоком управления, могут быть объединены в один функциональный блок:

Второй тип потока управления называется ветвлением - он организует выполнение одного из двух функциональных блоков в зависимости от значения проверяемого логического условия. Блок-схема структуры:

Понятие структурный подход. Для разработки алгоритма сложных задач используется принцип структурного проектирования алгоритмов.  Структурный подход к созданию алгоритмов - это метод разработки алгоритма, который обеспечивает легкость чтения алгоритма, простоту проверки правильности выполнения алгоритма, удобство его модификации.

Этот метод предусматривает:

• конструирования алгоритма с использованием трех базовых алгоритмических структур;  • использование метода пошаговой детализации, т.е. измельчение задачи на более простые задачи, затем измельчения этих задач на еще более простые составляющие и т. д. (разработка алгоритма «сверху вниз»);  • анализ алгоритма, т.е. контроль правильности каждой структуры алгоритма и взаимосвязей структур.  Преимуществом структурного подхода является его модульность. Модуль - это последовательность логически связанных команд, которая оформлена в виде отдельного алгоритма. Эти вспомогательные алгоритмы можно конструировать и анализировать отдельно и независимо, используя их затем в основном алгоритме или других вспомогательных алгоритмах. 

Эффективность алгоритмов

Рекурсия и эффективность алгоритмов. Рекурсивное программирование дает нам общий подход к решению задач – разбиению их на аналогичные подзадачи меньшей размерности, либо на задачи, представляющие собой шаги в возможных направлениях ее решения. Так или иначе, рекурсивные вызовы образуют древовидную структуру, количество вершин в которой определяет эффективность алгоритма (выражаемую обычно через трудоемкость). Разница между различными типами алгоритмов состоит в способе получения подзадач, их размерности, способе соединения полученных результатов.

        рекурсивное или обычное разделение. Идея разделения восходит к технологическому приему - модульному программированию (3.6). В своем первоначальном варианте она предполагает разбиение на задачи различной природы. Нерекурсивное разделение позволяет достичь определенного эффекта за счет разбиения задачи на множество идентичных задач меньшей размерности с последующим объединением результата. Типичным примером здесь является сортировка однократным слиянием (4.6). Применение того же самого алгоритма рекурсивно к полученным подзадачам дает следующий класс алгоритмов – рекурсивное разделение. Как правило, независимость полученных подзадач подразумевает соответствующее разделение исходных данных задачи на непересекающиеся подмножества – этому и соответствует сам термин разделение. Эффективность (и трудоемкость) таких алгоритмов, зависит от затрат на само разделение и от пропорций разделяемых частей: лучшему случаю соответствует деление на равные части (логарифмические зависимость),  худшему – выделение единственного элемента (линейные зависимости).

        жадные алгоритмы. Идеальным случаем можно считать алгоритм, способный  «выбрать из нескольких зол» единственно правильное. В основе его так же лежит принцип разделения, но в каждой точке он  имеет основание выбрать одну из подзадач. Обычно это делается на основании особенностей организации обрабатываемых данных или их избыточности. Типичный пример: двоичный поиск в упорядоченных данных (4.6). Основой жадных алгоритмов является всегда довольно спорное утверждение: движение «по линии наименьшего сопротивления» в каждой точке приведет к желаемому результату.

        полный перебор (исчерпывающий, комбинаторный перебор).  Перечисленные выше подходы основаны на всевозможных «ухищрениях», основанных на особенностях предметной области алгоритма. Если же ничего не помогает, то остается полный перебор всех возможных вариантов решения задачи (8.4).

        динамическое программирование. В процессе порождения дерева рекурсивных вызовов  возможно повторение подзадач с одними и теми же данными. Если запоминать результат их выполнения, то эффективность алгоритма может быть значительно увеличена.

Проверка правильности программ

Тести́рование програ́ммного обеспе́че́ния — процесс исследования, испытания программного продукта, имеющий две различные цели:

• продемонстрировать разработчикам и заказчикам, что программа соответствует требованиям;

• выявить ситуации, в которых поведение программы является неправильным, нежелательным или не соответствующим спецификации^[1].

По объекту тестирования

• Функциональное тестирование

• Тестирование производительности

  • Нагрузочное тестирование

  • Стресс-тестирование

  • Тестирование стабильности

• Конфигурационное тестирование

• Юзабилити-тестирование

• Тестирование интерфейса пользователя

• Тестирование безопасности

• Тестирование локализации

• Тестирование совместимости

По знанию системы

• Тестирование чёрного ящика

• Тестирование белого ящика

• Тестирование серого ящика

По степени автоматизации

• Ручное тестирование

• Автоматизированное тестирование

• Полуавтоматизированное тестирование

По степени изолированности компонентов

• Модульное тестирование

• Интеграционное тестирование

• Системное тестирование

По времени проведения тестирования^{[источник не указан 196 дней]}

• Альфа-тестирование

  • Дымовое тестирование (англ. smoke testing)

  • Тестирование новой функции (new feature testing)

  • Подтверждающее тестирование

  • Регрессионное тестирование

  • Приёмочное тестирование

• Бета-тестирование

По признаку позитивности сценариев

• Позитивное тестирование

• Негативное тестирование

По степени подготовленности к тестированию

• Тестирование по документации (формальное тестирование)

• Интуитивное тестирование (англ. ad hoc testing)

Теория графов и мографов

Понятие графов

Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными.  Если ребра ориентированны, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом.  Если ребра не имеют ориентации, граф называется неориентированным.

Граф

Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра - линиями, соединяющими точки (рис. 2.15).

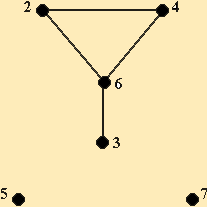
Рис. 2.15

Петля это дуга, начальная и конечная вершина которой совпадают.

Простой граф граф без кратных ребер и петель.

Степень вершины это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер.

Пустым называется граф без ребер. Полным называется граф, в котором каждые две вершины смежные.

Виды графов

Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом (рис. 1). Если же граф связный, но это условие не выполняется, тогда такой граф называетсяориентированным или орграфом (рис. 2).

В ориентированных и неориентированных графах имеется понятие степени вершины. Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для рисунка 2 сумма всех степеней равна 20.

 

 

В орграфе, в отличие от неориентированного графа, имеется возможность двигаться из вершины h в вершину s без промежуточных вершин, лишь тогда когда ребро выходит из h и входит в s, но не наоборот.

Ориентированные графы имеют следующую форму записи:

G=(V, A), где V – вершины, A – направленные ребра.

Третий тип графов – смешанные графы (рис. 3). Они имеют как направленные ребра, так и ненаправленные. Формально смешанный граф записывается так: G=(V, E, A), где каждая из букв в скобках обозначает тоже, что ей приписывалось ранее.

 

Матрицы смежности и инцидентности

На рис 3.12 изображено множество точек V и множество линий E, соединяющих эти точки, которые все вместе образуют граф Г. Если линии имеют стрелки, то граф называется ориентированным или орграфом Г₀ (рис. 3.13). Внутренних различий между Г и Г₀ гораздо меньше, чем между графом, изображающим правильную решетку из подгрупп для какой-нибудь группы, например,S(  ) (рис. 2.18), и графом, изображающим сильно неправильную метарешетку M₁₆ (рис. 2.26).

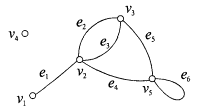
Рис. 3.12

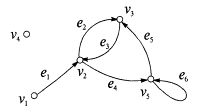
Рис. 3.13

Внешняя морфология графа (со стрелками или без них) играет подчиненную роль, математическая же сущность представленного графом объекта всегда остается где-то за рамками рисунка. Изображение графа в большинстве случаев является проекцией или тенью этой сущности и самостоятельного значения не имеет. Однако морфология расположения точек и линий, тем не менее, поддается определенной математической классификации и описанию. Этим мы намерены заняться в этом и последующем подразделах.

Линии в графе Г здесь и далее будем называть ребрами, а ориентированные линии в орграфе Г₀ — дугами. О вершинах и ребрах (дугах) говорят, что они инцидентны, если вершина принадлежит ребру (дуге); если вершина не инцидентна никакому ребру (дуге), то она называется изолированной (v₄). Путь называется простым, если никакая дуга или ребро не встречается в нем дважды. Путь называется элементарным, если никакая вершина в нем не встречается дважды.

Цикл — это замкнутый путь в неориентированном графе. Контур — это ориентированный цикл в орграфе. Понятия простоты и элементарности распространяются на циклы и контуры. Контур или цикл, который содержит все ребра или дуги графа, называется эйлеровым. Можно показать, что связанный орграф (т.е. без изолированных фрагментов) содержит эйлеров контур тогда и только тогда, когда для каждой вершины число входящих дуг равно числу выходящих; связанный неориентированный граф содержит эйлеров цикл тогда и только тогда, когда степень каждой вершины четна. Степенью (валентностью) вершины называется число инцидентных ей ребер. Простой путь, который проходит через все вершины графа, называется гамильтоновым. Если в простом графе с n вершинами степень каждой вершины не меньше n/2, то такой граф обязательно будет гамильтоновым. Однако легко построить гамильтонов граф, у которого степень вершины меньше n/2.

Графы Г и Г₀ можно представить в аналитической форме либо матрицей смежности A, либо матрицей инцидентности B. Для нашего конкретного неориентированного графа Г матрицы A и B выглядят следующим образом:

A(Г) =	B(Г) =

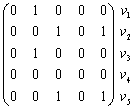
Матрица смежности для неориентированного графа всегда симметрична. Фигурирующая в ней 2 может быть в некоторых случаях заменена на 1. В матрице инцидентности сумма единиц по столбцам указывает на степень вершины v_i. Нередко расположение вершин и ребер в этой матрице меняют местами (транспонируют). Так, для нашего конкретного орграфа Г₀ матрица A и B выглядят иначе:

A(Г0 ) =	B(Г0 ) =

Пути в графе

Путь в графе — последовательность вершин, имеющая для каждой вершины ребро, соединяющее её со следующей вершиной в последовательности.

Два пути вершинно независимы, если они не имеют общих внутренних вершин. Аналогично два пути рёберно независимы, если они не имеют общих внутренних рёбер.

Длина пути — это число рёбер, используемых в пути, при этом многократно используемые рёбра считаются соответствующее число раз. Длина может равняться нулю, если путь состоит из одной только вершины.

Взвешенный граф ставит в соответствие каждому ребру некоторое значение (вес ребра). Весом пути во взвешенном графе называется сумма весов рёбер пути. Иногда вместо слова вес употребляется цена или длина.

Пустые и полные подграфы

Пусть имеется граф G, обладающий свойствомP. Будем говорить, что графG являетсяP-минимальным, если не существует подграфа , обладающего этим свойством. ГрафG называетсяP-максимальным, если не существует надграфа , который обладает свойствомP. Например, на данном множестве вершин дерево является минимальным связным и максимальным графом без циклов. Слова «наибольший» и «наименьший» будем использовать для обозначения части графа, обладающей свойствомPи имеющей наибольшую (наименьшую) мощность.

Сети

Сетью называется граф, элементам которого поставлены в соответствие некоторые параметры. Далее элементы множества R будем называть узлами, а  множества   – дугами. Пусть  каждой  дуге   некоторой сети   поставлено в соответствие неотрицательное (действительное) число   ,  называемое  пропускной  способностью  дуги   . Функция  , отображающая множество   в множество неотрицательных чисел, называется функцией пропускной способности. Пусть s и t – два различных узла из R. Стационарный поток величины v из s в t в сети    есть функция f, отображающая множество А  в множество неотрицательных чисел, удовлетворяющая линейным уравнениям и неравенствам

Раскраска графов

В теории графов, раскраска графов является частным случаем разметки графов. При раскраске элементам графа ставятся в соответствие метки с учетом определенных ограничений; эти метки традиционно называются “цветами”. В простейшем случае, такой способ окраски вершин графа, при котором любым двум смежным вершинам соответствуют разные цвета, называетсяраскраской вершин. Аналогично, раскраска ребер присваивает цвет каждому ребру так, чтобы любые два смежных ребра имели разные цвета.^[1] Наконец, раскраска областей планарного графа назначает цвет каждой области, так, что каждые две области, имеющие общую границу, не могут иметь одинаковый цвет.

Раскраска вершин – главная проблема раскраски графов, все остальные задачи в этой области могут быть перенесены на эту модель. Например, раскраска ребер графа - это раскраска вершин его рёберного графа, а раскраска областей планарного графа – это раскраска вершин двойственного графа.^[1] Тем не менее, другие проблемы раскраски графов часто ставятся и решаются в изначальной постановке. Причина этого частично заключается в том, что это даёт лучшее представление о происходящем и более показательно, а частично из-за того, что некоторые задачи таким образом решать удобнее (например, раскраска ребер).

Договоренность об использовании цветов происходит из традиции выделения цветом стран на политической карте.^[1] Она была обобщена на окраску областей планарного графа. Через двойственные графы эта модель распространилась и на раскраску вершин, а затем и на другие виды графов. В математическом и компьютерном представлении обычно в качестве цветов используются целые неотрицательные числа (от нуля и больше). Таким образом, мы можем использовать любой конечный набор в качестве “цветового набора”, и проблема раскраски графов зависит от количества цветов, а не от того, чем они являются.

Дискретная математика

Теория множеств

Понятие множества является исходным не определяемым строго понятием. Приведем здесь определение множества (точнее, пояснение идеи множества), принадлежащее Г. Кантору: "Под многообразием или множеством я понимаю вообще все многое, которое возможно мыслить как единое, т.е. такую совокупность определенных элементов, которая посредством одного закона может быть соединена в одно целое".

Множества будем, как правило, обозначать большими буквами латинского алфавита, а их элементы — малыми, хотя иногда от этого соглашения придется отступать, так как элементами некоторого множества могут быть другие множества. Тот факт, что элемент а принадлежит множеству  , записывается в виде  .

В математике мы имеем дело с самыми различными множествами. Для элементов этих множеств мы используем два основных вида обозначений: константы и переменные.

Индивидная константа (или просто константа) с областью значений   обозначает фиксированный элемент множества  . Таковы, например, обозначения (записи в определенной системе счисления) действительных чисел:  . Для двух констант   и   с областью значений   будем писать  , понимая под этим совпадение обозначаемых ими элементов множества  .

Индивидное переменное (или просто переменное) с областью значений   обозначает произвольный, заранее не определенный элемент множества  . При этом говорят, что переменное   пробегает множество   или переменное   принимает произвольные значения на множестве  . Можно фиксировать значение переменного  , записав  , где   — константа с той же областью значений, что и  . В этом случае говорят, что вместо переменного  подставлено его конкретное значение  , или произведена подстановка   вместо  , или переменное   приняло значение  .

Равенство переменных   понимается так: всякий раз, когда переменное   принимает произвольное значение  , переменное   принимает то же самое значение  , и наоборот. Таким образом, равные переменные "синхронно" принимают всегда одни и те же значения.

Обычно константы и переменные, область значений которых есть некоторое числовое множество, а именно одно из множеств   и  , называют соответственно натуральными, целыми (или целочисленными), рациональными, действительными и комплексными константами и переменными. В курсе дискретной математики мы будем использовать различные константы и переменные, область значений которых не всегда является числовым множеством.

Для сокращения записи мы будем пользоваться логической символикой, позволяющей коротко, наподобие формул, записывать высказывания. Понятие высказывания не определяется. Указывается только, что всякое высказывание может быть истинным или ложным (разумеется, не одновременно!).

Отношения

 Подмножество  называется местным (мерным) отношением на множестве А. Говорят, что элементы находятся в отношении , если .

Одноместное (одномерное) отношение — это просто некоторое подмножество А. Такие отношения называют признаками. Говорят, что  обладает признаком , если  и . Свойства одноместных отношений — это свойства подмножеств А, поэтому для случая  термин “отношения” употребляется редко.

Наиболее часто встречающимися и хорошо изученными являются двухместные или бинарные отношения. Если  и  находятся в отношении , это обычно записывается в виде .

Пример 1. Бинарные отношения на множестве .

а) Отношение “” выполняется для пар  и не выполняется для пары .

б) Отношение “иметь общий делитель, не равный единице” выполняется для пар  и не выполняется для пар .

в) Отношение “быть делителем” выполняется для пар  и не выполняется для пар .

Пример 2. Бинарные отношения на множестве точек координатной плоскости.

а) Отношение “быть равноудалёнными от начала координат” выполнятся для пар точек  и , но не выполнятся для пары точек  и .

б) Отношение “принадлежать окружности, центр которой находится в начале координат”, выполняется для первой пары точек из предыдущего примера и не выполняется для второй пары.

в) Отношение “быть удалёнными на разное расстояние от начала координат” выполняется для всех точек, для которых не выполняется отношение, описанное в пункте “б”.

Пусть дано отношение  на множестве А. Для любого подмножества  определяется отношение , называемое сужением  на , которое получается из отношения  удалением всех пар, содержащих элементы, не принадлежащие . Иначе говоря, .

Строго говоря, само отношение  и его сужение  - это разные отношения, с разными областями определения. Однако, по умолчанию, если не возникает явных разночтений, эта разница не учитывается. Например, вполне можно говорить об отношении “быть делителем”, не уточняя, задано оно на множестве  или на каком-нибудь его подмножестве.

Для задания бинарных отношений можно использовать любые способы задания множеств (например, список пар, для которых данное отношение выполняется). Отношения на конечных множествах обычно задаются списком или матрицей. Матрица бинарного отношения на конечном множестве  - это квадратная матрица  порядка , в которой каждый элемент  определяется следующим образом:

Моделирование

Понятие моделирование

Моделирование можно рассматривать как замещение исследуемого объекта (оригинала) его условным образом, описанием или другим объектом, именуемым моделью и обеспечивающим близкое к оригиналу поведение в рамках некоторых допущений и приемлемых погрешностей. Моделирование обычно выполняется с целью познания свойств оригинала путем исследования его модели, а не самого объекта. Разумеется, моделирование оправдано в том случае когда оно проще создания самого оригинала или когда последний по каким-то причинам лучше вообще не создавать.

Под моделью понимается физический или абстрактный объект, свойства которого в определенном смысле сходны со свойствами исследуемого объекта. При этом требования к модели определяются решаемой задачей и имеющимися средствами [19]. Существует ряд общих требований к моделям:

1. Адекватность – достаточно точное отображение свойств объекта;

2. Полнота – предоставление получателю всей необходимой информации об объекте;

3. Гибкость – возможность воспроизведения различных ситуаций во всем диапазоне изменения условий и параметров;

4. Трудоемкость разработки должна быть приемлемой для имеющегося времени и программных средств.

Моделирование – это процесс построения модели объекта и исследования его свойств путем исследования модели.

Классификация моделей

 Признаки классификаций моделей: 1) по области использования;

   2) по фактору времени;

   3) по отрасли знаний;

   4) по форме представления