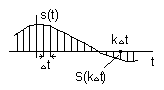- •Преимущества дискретной формы
- •Представление информации в цифровых автоматах. Информация и алфавит. Кодирование.
- •Код Шеннона-Фано
- •Код Хаффмана Кодирование Хаффмана[править | править вики-текст]
- •Кодирование в компьютере чисел со знаком Прямой код
- •Дополнительный код
- •Операция сложения положительного числа и отрицательного числа, представленного в прямом коде
- •Операция сложения положительного числа и отрицательного числа, представленного в дополнительном коде
- •Кодирование вещественных чисел. Нормализованное представление числа
- •Описание[править | править вики-текст]
- •Преимущества и недостатки[править | править вики-текст] Преимущества[править | править вики-текст]
- •Недостатки[править | править вики-текст]
- •1) Классификация моделей по области использования:
- •2) Классификация моделей по фактору времени:
- •Особенности алгоритмов управления ресурсами
- •Особенности аппаратных платформ
- •Особенности областей использования
- •Особенности методов построения
- •Монолитное ядро[править | править вики-текст]
- •Модульное ядро[править | править вики-текст]
- •Микроядро[править | править вики-текст]
- •Экзоядро[править | править вики-текст]
- •Наноядро[править | править вики-текст]
- •Гибридное ядро[править | править вики-текст]
- •Физическая организация памяти компьютера
- •Классификация процессоров:
- •Классификация по назначению
- •Классификация по характеру временной организации работы
- •Классификация по количеству выполняемых программ
- •Конвейеризация - способ обеспечения параллельности выполнения команд
- •O Аппаратное обеспечение компьютера – это группа взаимосвязанных устройств, предназначенных для приема, преобразования и выдачи информации.
- •Ускорение вычислений.
- •Вычислительные системы с программируемой структурой
- •Требования, предъявляемые к инфологической модели
- •Архитектура odmg
- •1.2. Домен
- •1.3. Схема отношения, схема базы данных
- •1.4. Кортеж, отношение
- •7.2.1. Общие определения
- •7.2.2. Замыкание множества функциональных зависимостей. Аксиомы Армстронга. Замыкание множества атрибутов
- •Пересечение
- •Разность
- •Структура памяти эвм
- •По порядку сортировки
- •По источнику данных
- •По воздействию на источник данных
- •По структуре
- •По количественному составу
- •По характеристике содержимого
- •По механизму обновления
- •По покрытию индексируемого содержимого
- •3.3. Виды привилегий
- •Стандарт iso 7498
- •Асинхронная передача.
- •Синхронная передача.
- •Кабельные линии связи
- •Беспроводные (радиоканалы наземной и спутниковой связи) каналы передачи данных
- •Технология скремблирования
- •Селективные методы
- •Методы случайного доступа
- •Методы резервирования времени
- •Технология доступа[править | править вики-текст]
- •Обнаружение коллизий[править | править вики-текст]
- •Формат кадра
- •Разновидности Ethernet
- •Структура Fast Ethernet
- •Подуровень управления логической связью (llc)
- •Новые интерфейсы и модель физического уровня
- •Типы спецификаций 10-гигабитного Ethernet
- •Объединение сетей в интерсеть. Удаленный мост
- •Формат сообщения протокола rip 1
- •Формат сообщения протокола rip 2
- •1.1. Назначение протокола arp. Arp-таблицы. Статические и динамические записи arp-таблиц, arp-кэш
- •3.2. Формат icmp-пакета
Формы представления данных. Текстовая информация (тексты в учебниках, статьи), числовая информация (арифметические операции числа и прочее), графическая информация (рисунки, схемы чертежи), звуковая информация(сообщения), мультимедийная(сочетание графической и звуковой).
Преобразование непрерывных сообщений. Теорема Котельникова. При передаче непрерывных сообщений по системам связи c использованием импульсной модуляции или кодирования возникает необходимость дискретизации сообщений по времени. В последнее время необходимость дискретизации непрерывных сигналов объясняется развитием методов квантования, дискретного анализа формы сигналов, развитием цифровой и вычислительной техники.
|
Сущность дискретизации заключается в том, что непрерывность во времени функции s(t) заменяется последовательностью коротких импульсов, амплитуды которых (координаты) ск в общем случае определяются с помощью |
дискретных
весовых функций xк(t) ![]() .
.
Воспроизведение
непрерывной функции по ее дискретным
координатам производится с помощью
системы базисных функций ![]()
![]() Иногда
весовые и базисные функции принимают
одинаковыми
Иногда
весовые и базисные функции принимают
одинаковыми ![]() Ввиду
сложности определения координатных
функций более широкое распространение
получили методы дискретизации, при
которых сигнал s(t)заменяется
совокупностью его мгновенных значений
Ввиду
сложности определения координатных
функций более широкое распространение
получили методы дискретизации, при
которых сигнал s(t)заменяется
совокупностью его мгновенных значений ![]() ,
называемых выборками, или отсчетами.
Роль весовых функций в этом случае
играют d-функции
,
называемых выборками, или отсчетами.
Роль весовых функций в этом случае
играют d-функции ![]() , Dt - шаг
дискретизации (может быть неравномерным).
, Dt - шаг
дискретизации (может быть неравномерным). ![]() .
Шаг дискретизации должен быть таким,
чтобы было возможно восстановление
непрерывной функции по ее отсчетам с
допустимой точностью.
.
Шаг дискретизации должен быть таким,
чтобы было возможно восстановление
непрерывной функции по ее отсчетам с
допустимой точностью.
Равномерная дискретизация. Теорема Котельникова
Правило
выбора предельного шага при равномерной
дискретизации с использованием модели
сигнала с ограниченным спектром
сформулировано академиком В. А.
Котельниковым: «Любая непрерывная
функция s(t), спектр которой ограничен
частотой Fmax полностью определяется
последовательностью своих значений в
моменты времени, отстоящие друг от друга
на интервал![]() »
Кроме того, теорема Котельникова дает
и способ точного восстановления
сигнала
»
Кроме того, теорема Котельникова дает
и способ точного восстановления
сигнала ![]() по
его отсчетам.
по
его отсчетам.
Доказательство
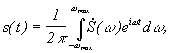 причем
причем ![]() при
при ![]() (1)
(1)
Разложим
функцию ![]() в
частотной области на конечном
интервале
в
частотной области на конечном
интервале ![]() (с
периодом
(с
периодом ![]() )
в комплексный ряд Фурье :
)
в комплексный ряд Фурье :
![]() где
(2)
где
(2)
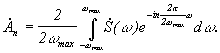 (3)
(3)
Сравнивая
интегралы в (3) и (1), видно, что они равны
при ![]() ,
т. е.
,
т. е.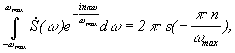 тогда
тогда
![]() (4)
(4)
Подставляем (4) в (2), а затем в (1)
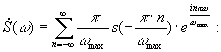
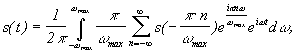
т. к. суммирование по от -¥ до +¥, то можно заменить знак у .
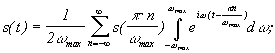
![]()
![]() (5)
(5)
Максимальные
значения членов ряда будут при ![]() и
равны
и
равны ![]() ,
при этом все остальные члены ряда равны
нулю, т. е. при
функция s(t) точно
передается рядом. Во все другие моменты
времени необходимо суммировать
бесконечное число отсчетов, чтобы
передать s(t) точно.
,
при этом все остальные члены ряда равны
нулю, т. е. при
функция s(t) точно
передается рядом. Во все другие моменты
времени необходимо суммировать
бесконечное число отсчетов, чтобы
передать s(t) точно.
Представление
сигнала в виде ряда Котельникова (5)
является частным случаем разложения ![]() .
Роль коэффициента
.
Роль коэффициента ![]() выполняют
отсчеты
выполняют
отсчеты ![]() Базисными
являются функции вида
Базисными
являются функции вида ![]() Они
называются функциями отсчетов. Функции
отсчетов ортогональны, т. к.
Они
называются функциями отсчетов. Функции
отсчетов ортогональны, т. к.
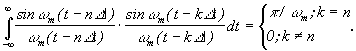
|
Спектральная
плотность функции отсчета на частотной
шкале есть прямоугольник
шириной Теорема Котельникова распространяется на непрерывный стационарный случайный процесс с ограниченным спектром
|
Такой процесс представляется (заменяется) суммой квазидетерминированных процессов, где роль ортогональных детерминированных функций выполняют функции отсчета, а случайных коэффициентов - величины выборок:
![]() ,
где
,
где ![]()
Т. о., при указанных ограничениях случайный процесс полностью определяется счетным множеством случайных величин - координат процесса. дискретизация непрерывных сигналов, преобразованиеэлектрического Сигнала, непрерывного во времени и по уровню, в последовательность дискретных(отдельных) либо дискретно-непрерывных сигналов, в совокупности отображающих исходный сигнал сзаранее установленной ошибкой. К. с. осуществляется при передаче данных в телемеханике, при аналого-цифровом преобразовании в вычислительной технике, в импульсных системах автоматики и др.
При передаче непрерывных сигналов обычно достаточно передавать не сам сигнал, а лишьпоследовательность его мгновенных значений, выделенных из исходного сигнала по определённому закону.К. с. производится по времени, уровню или по обоим параметрам одновременно. При К. с. по временисигнал через равные промежутки времени М прерывается (импульсный сигнал) либо изменяется скачком(ступенчатый сигнал, рис.). Например, непрерывный сигнал, проходя через контакты периодическивключаемого электрического реле, преобразуется в последовательность импульсных сигналов. Прибесконечно малых интервалах включения (отключения), т. е. при бесконечно большой частоте переключенийконтактов, получается точное представление непрерывного сигнала. При К. с. по уровню соответствующиемгновенные значения непрерывного сигнала заменяются ближайшими дискретными уровнями, которыеобразуют дискретную шкалу квантования. Любое значение сигнала, находящееся между уровнями,округляется до значения ближайшего уровня.
Преимущества дискретной формы
Основное преимущество цифровой информации перед аналоговой это помехозащищенность. То есть в процессе копирования информации цифровая информация копируется так как есть, её можно копировать практически бесконечное количество раз, аналоговая же информация в процессе копирования зашумляется, её качество ухудшается. Обычно аналоговую информацию можно копировать не более трех раз.
Представление информации в цифровых автоматах. Информация и алфавит. Кодирование.
В процессе переработки информации цифровые ЭВМ - компьютеры, оперируют числами, которые представляются в некоторой системе счисления. Система счисления - это совокупность приемов и правил для записи чисел цифровыми знаками. Запись числа в некоторой системе счисления часто называют кодом числа. Элементы (символы) алфавита, которые используются для записи чисел в некоторой системе счисления, принято называть цифрами. Каждой цифре данного числа однозначно сопоставляется ее количественный (числовой) эквивалент.
Алфавит — это множество (как правило конечное) символов или букв, например латинских букв и цифр. Примером распространённого алфавита является двоичный алфавит {0,1}. Конечная строка — это конечная последовательность букв алфавита. Например, двоичная строка — это строка из символов алфавита {0,1}. Также возможно построение бесконечных последовательностей из букв алфавита.
Позиционная система счисления (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда). Наиболее известной позиционной системой счисления является десятичная система счисления. Например, в десятичном числе 555 первая цифра справа означает 5 единиц, соседняя с ней - 5 десятков, а левая - 5 сотен.
Преобразование целых чисел
Для перевода необходимо исходное число разделить на основание новой системы счисления до получения целого остатка, который является младшим разрядом числа в новой системе счисления (единицы). Полученное частное снова делим на основание системы и так до тех пор, пока частное не станет меньше основания новой системы счисления. Все операции выполняются в исходной системе счисления.
Рассмотрим для примера перевод числа из десятичной системы счисления в двоичную систему счисления.
Возьмём десятичное число А10 = 124 и поделим его на основание двоичной системы, то есть число 2. Деление будем производить уголком:

В результате первого деления получим разряд единиц (самый младший разряд). В результате второго деления получим разряд двоек. Деление продолжаем, пока результат деления больше двух. В конце операции преобразования мы получили двоичное число 11111002.
Теперь то же самое число переведём в восьмеричную систему счисления. Для этого число 12410 разделим на число 8:

Как мы видим, остаток от первого деления равен 4. То есть младший разряд восьмеричного числа содержит цифру 4. Остаток от второго деления равен 7. то есть второй разряд восьмеричного числа – это цифра 7. Старший разряд получился равным 1. То есть в результате многократного деления мы получили восьмеричное число 1748.
Проверим, не ошиблись ли мы в процессе преобразования? Для этого преобразуем получившееся двоичное число в десятичную систему по обычной формуле разложения:
1×82+7×81+4×80=6410+5610+410=124
;А можно ли осуществить перевод из восьмеричной системы счисления в двоичную делением? Можно! Но деление нужно произвести по правилам восьмеричной арифметики. Правила работы в восьмеричной системе счисления мы рассмотрим в следующей главе. Тем не менее, для полноты материала, рассмотрим пример перевода в двоичную форму полученного ранее восьмеричного числа 1748. Разделим его на основание новой системы счисления 2.

Закодировать текст – значит сопоставить ему другой текст. Кодирование применяется при передаче данных – для того, чтобы зашифровать текст от посторонних, чтобы сделать передачу данных более надежной, потому что канал передачи данных может передавать только ограниченный набор символов (например, - только два символа, 0 и 1) и по другим причинам.
При кодировании заранее определяют алфавит, в котором записаны исходные тексты (исходный алфавит) и алфавит, в котором записаны закодированные тексты (коды), этот алфавит называется кодовым алфавитом. В качестве кодового алфавита часто используют двоичный алфавит, состоящий из двух символов (битов) 0 и 1. Слова в двоичном алфавите иногда называют битовыми последовательностями.