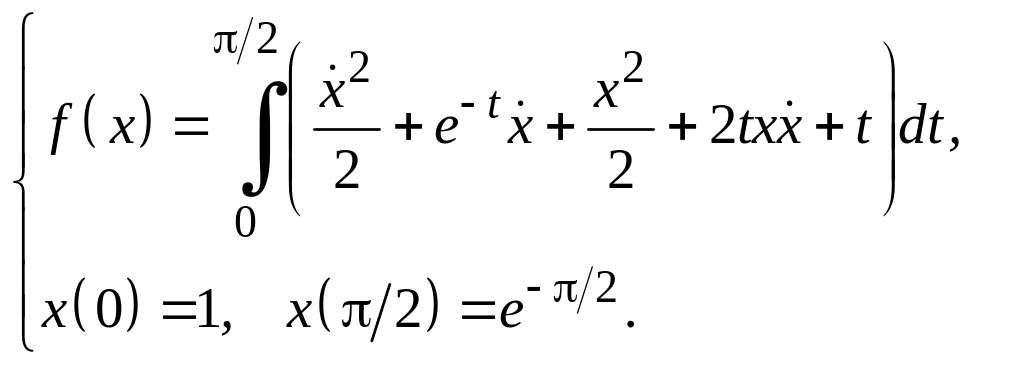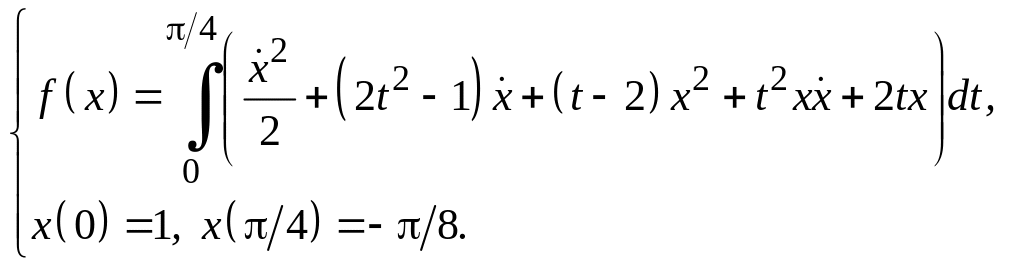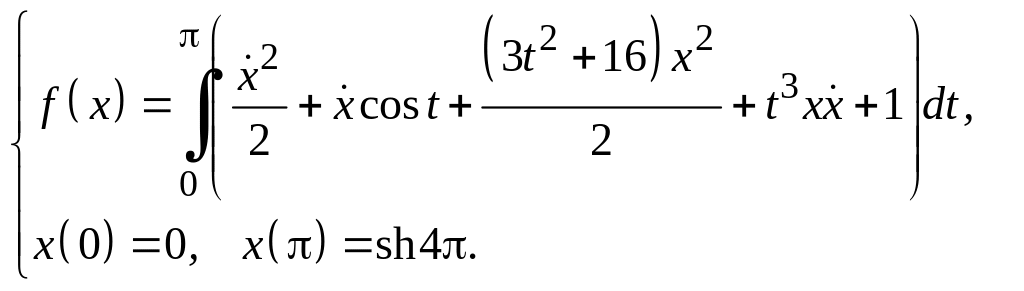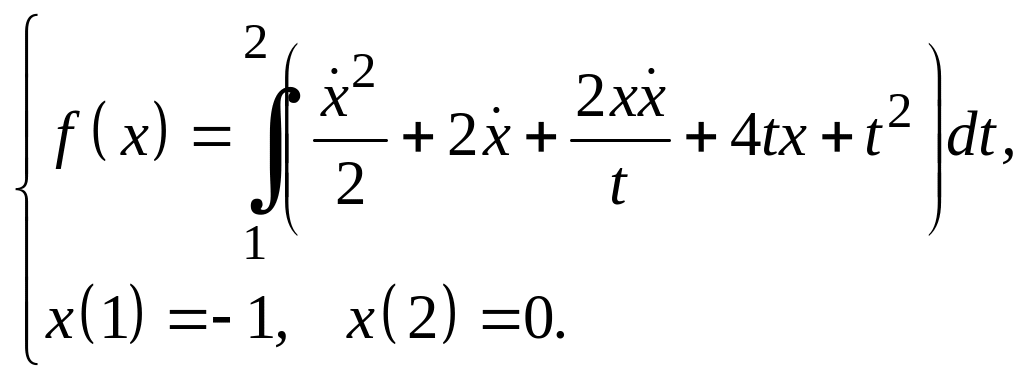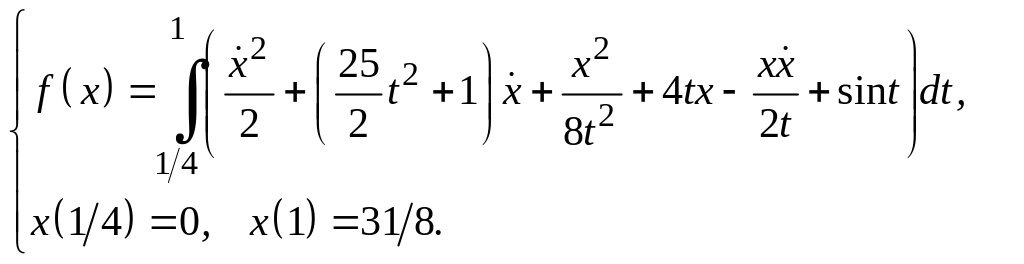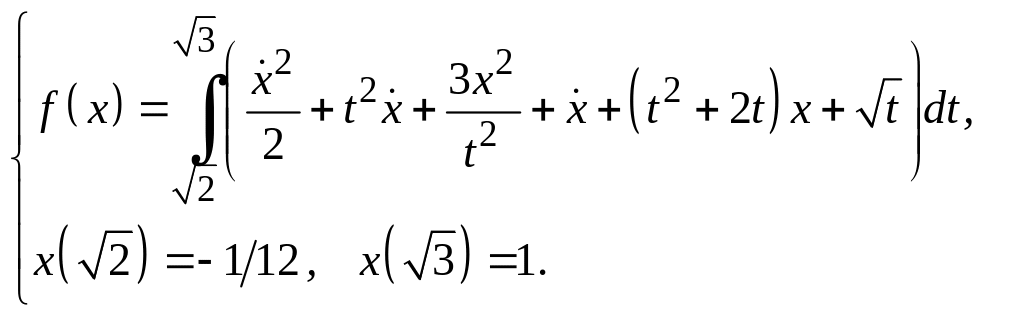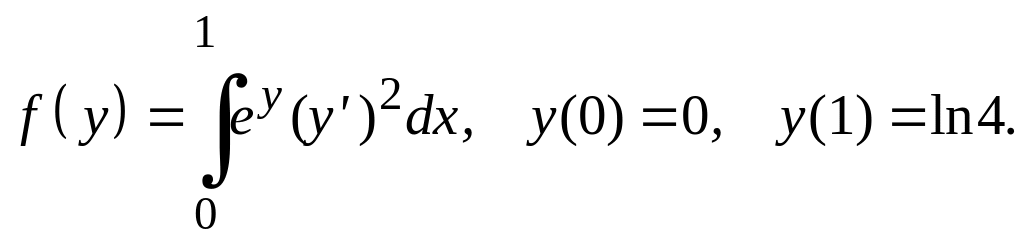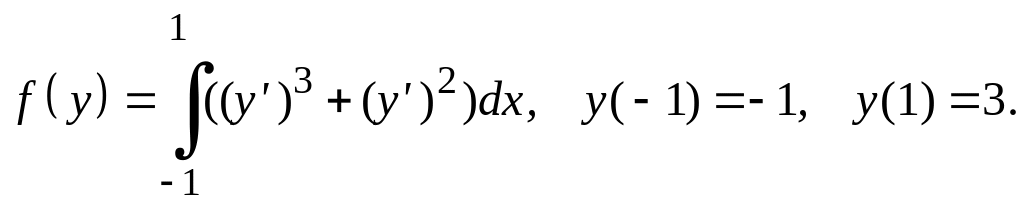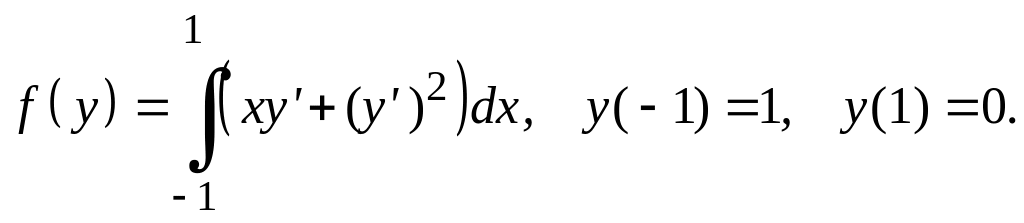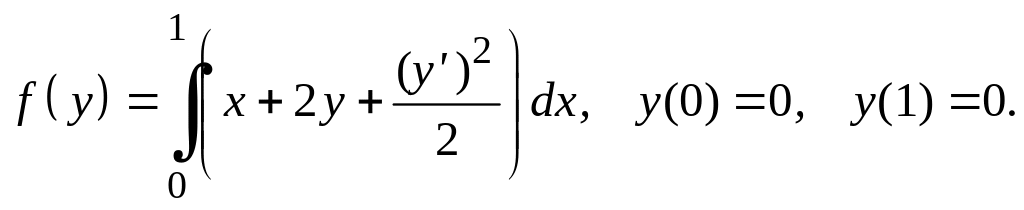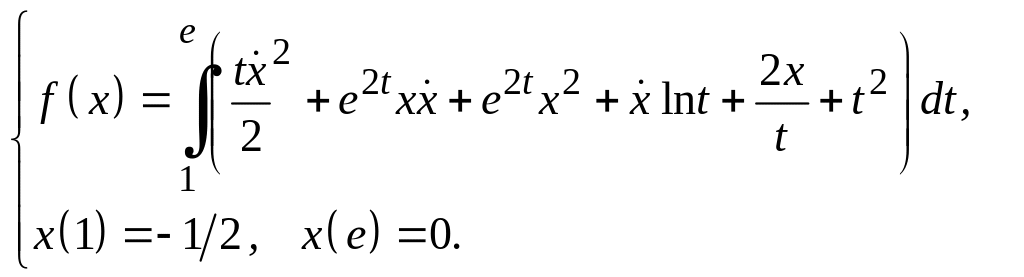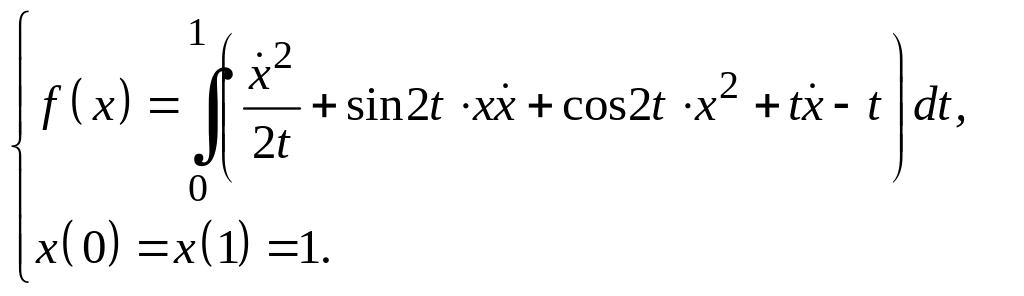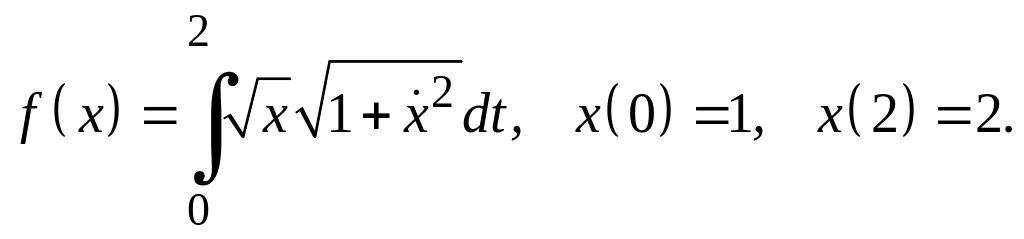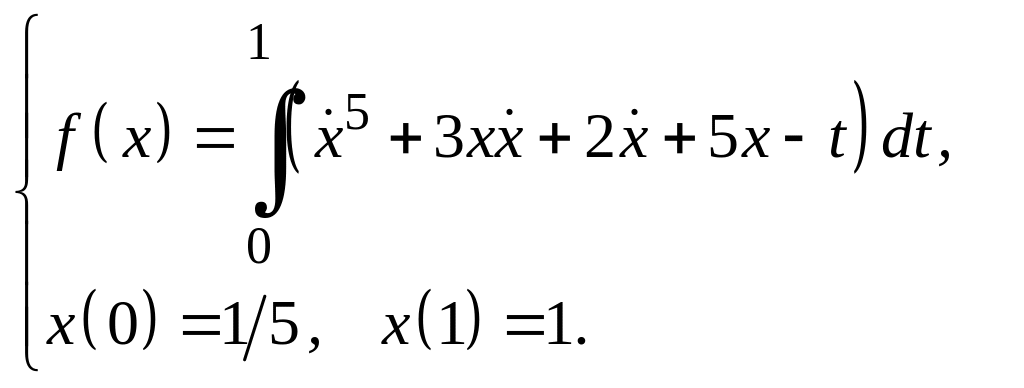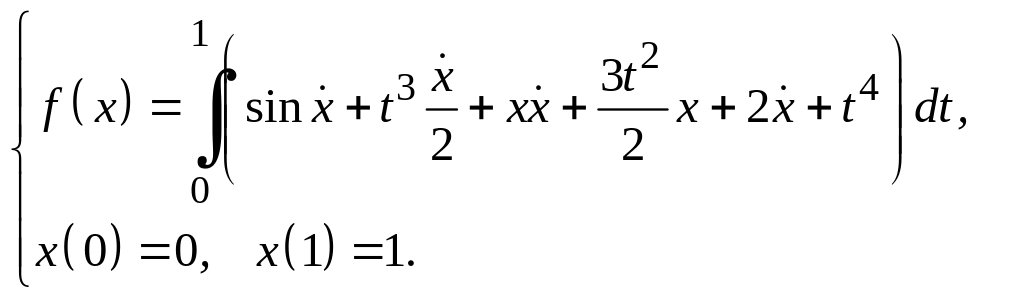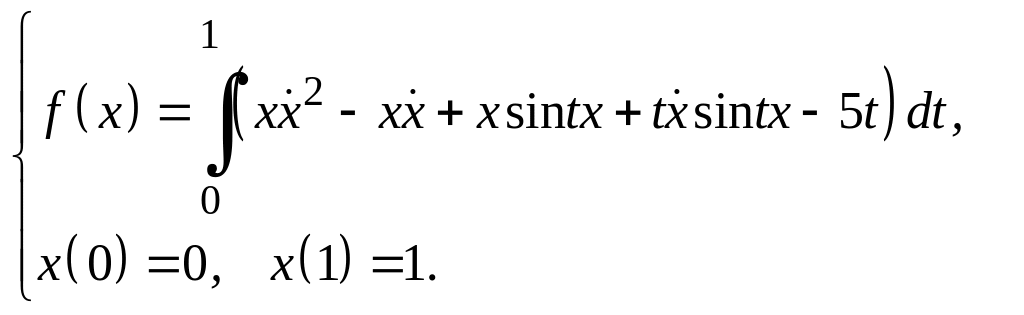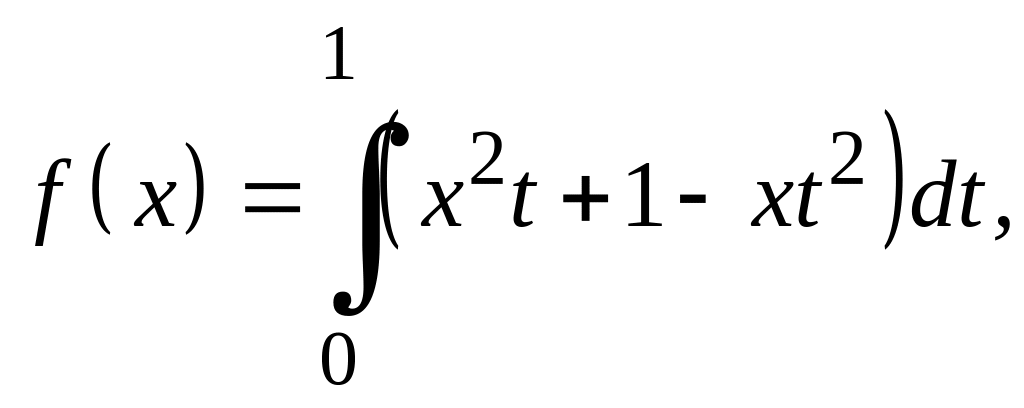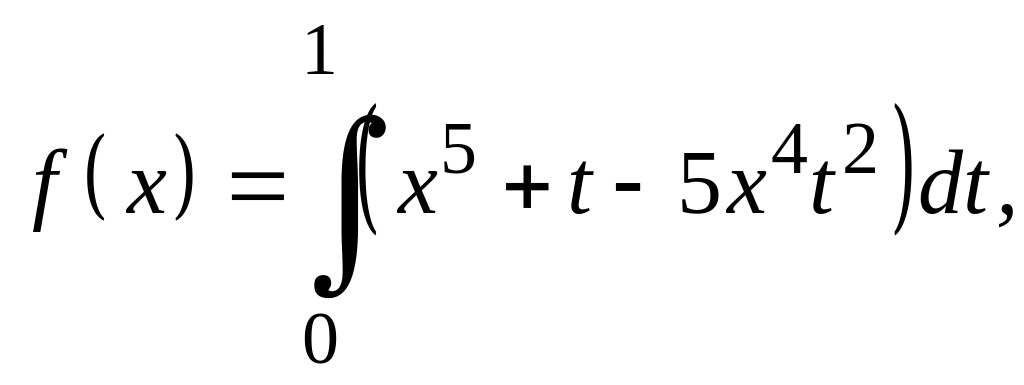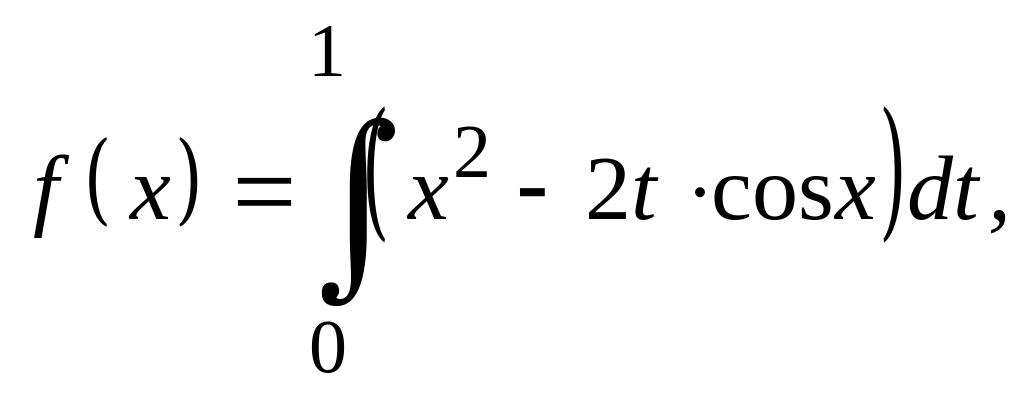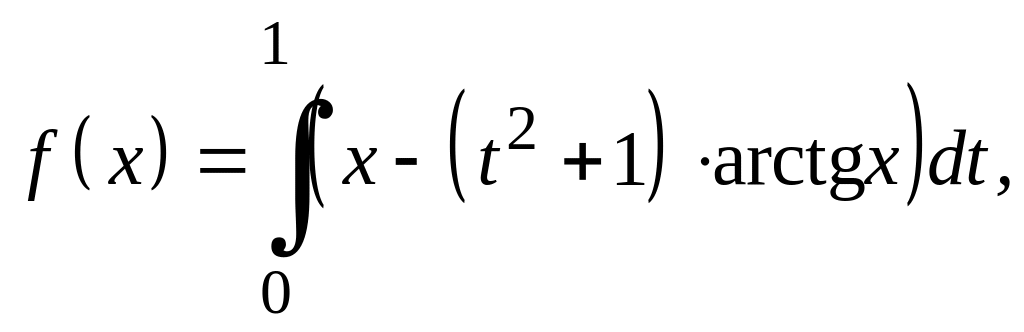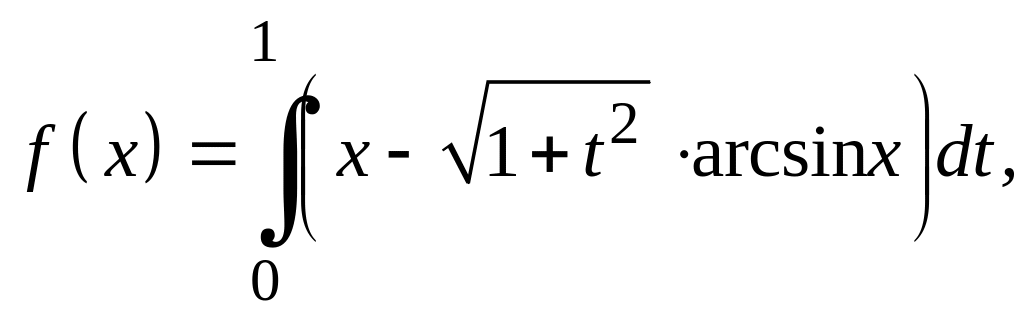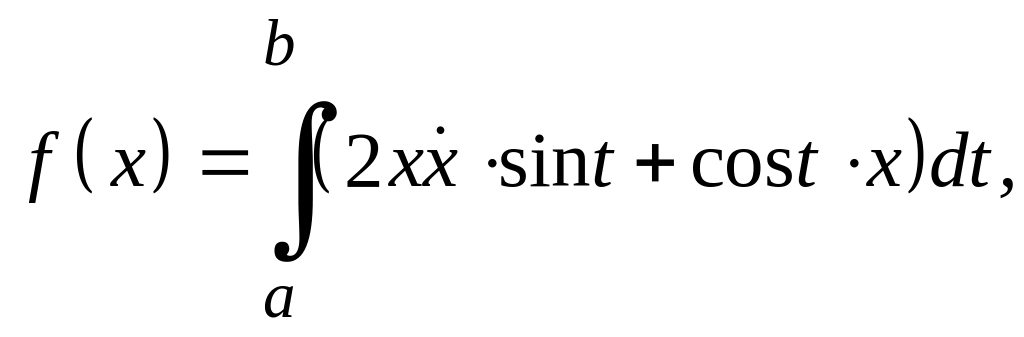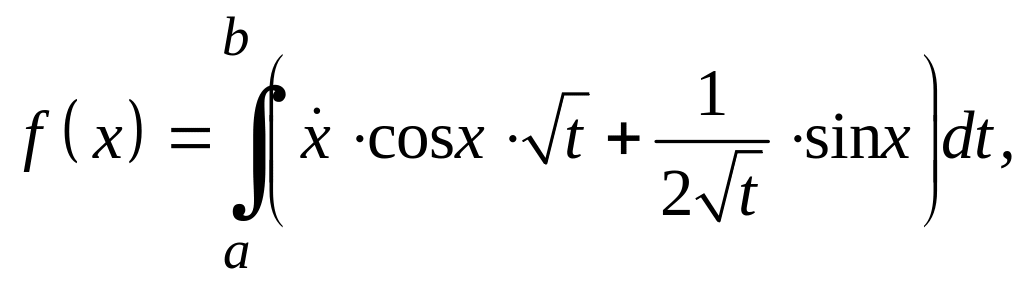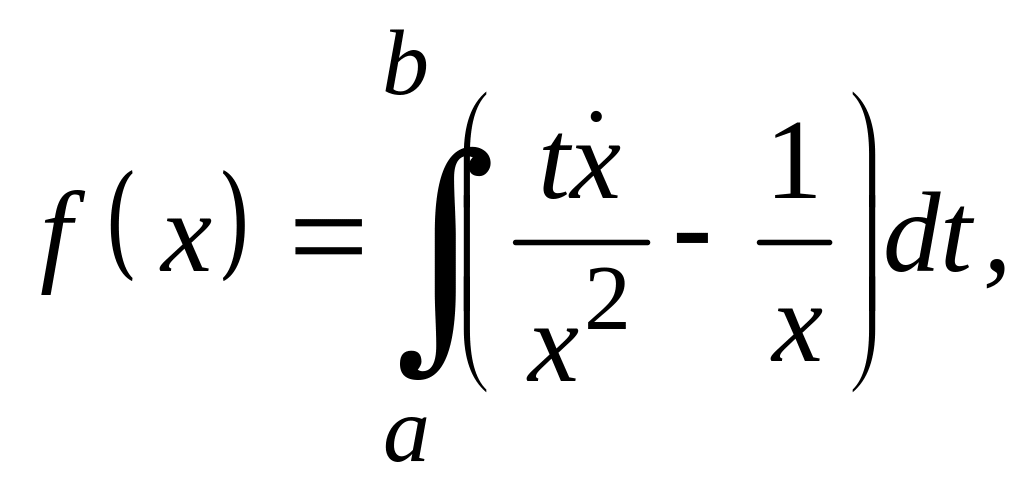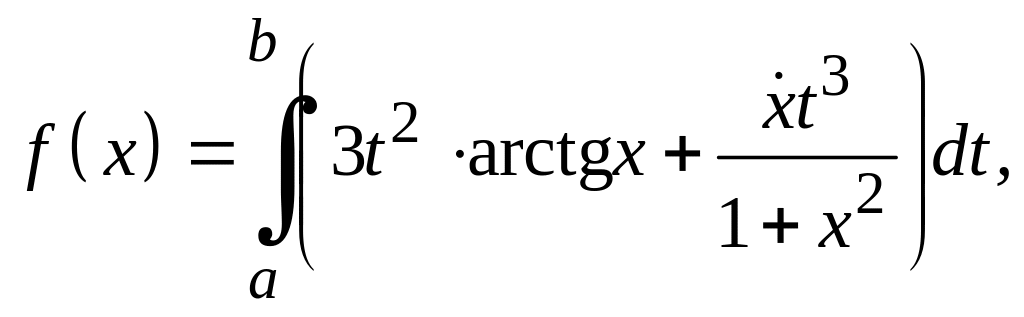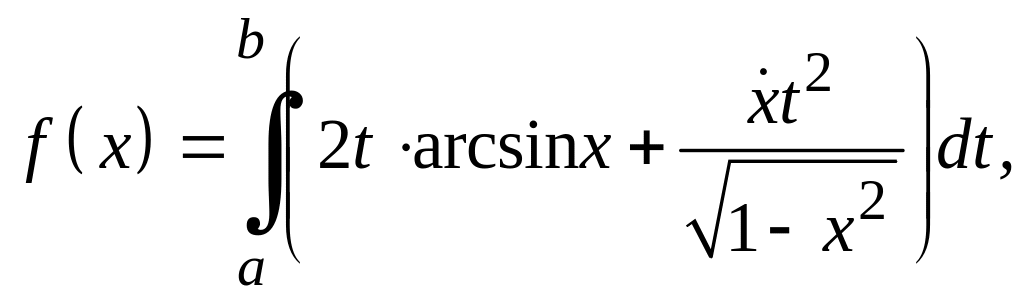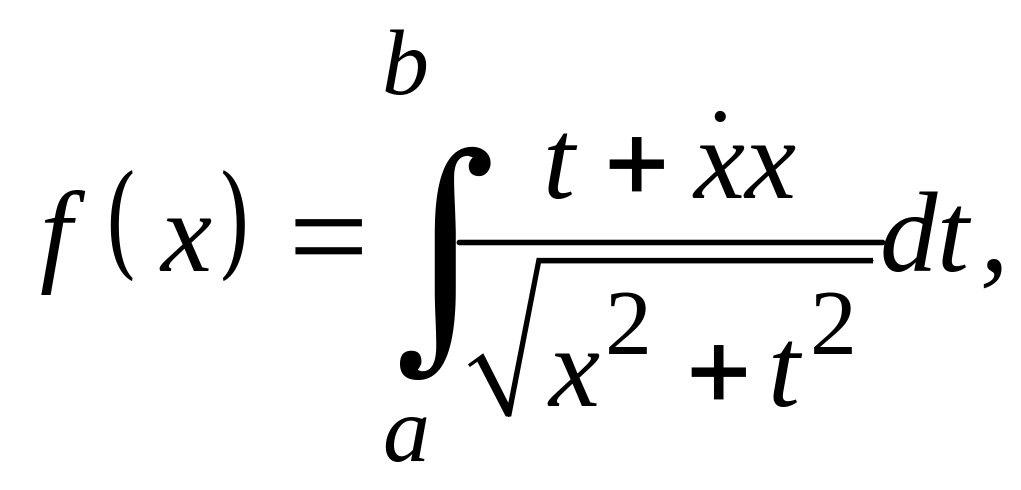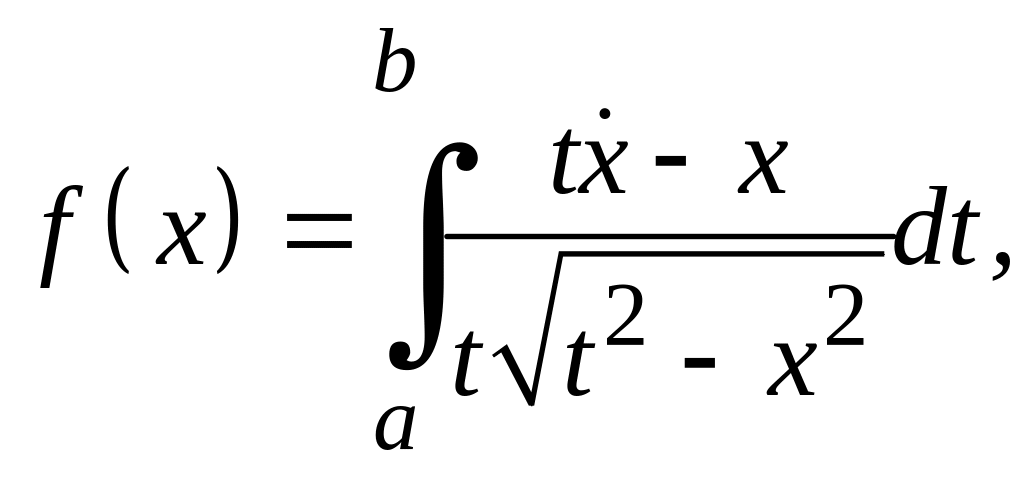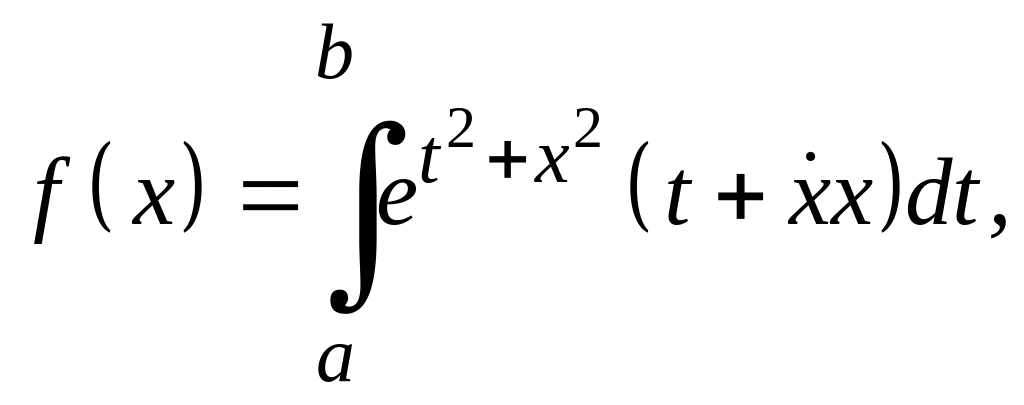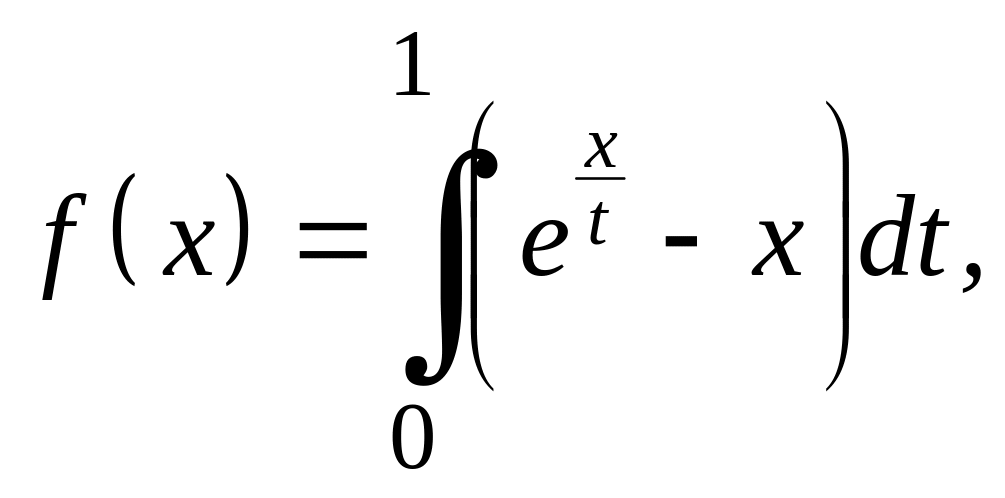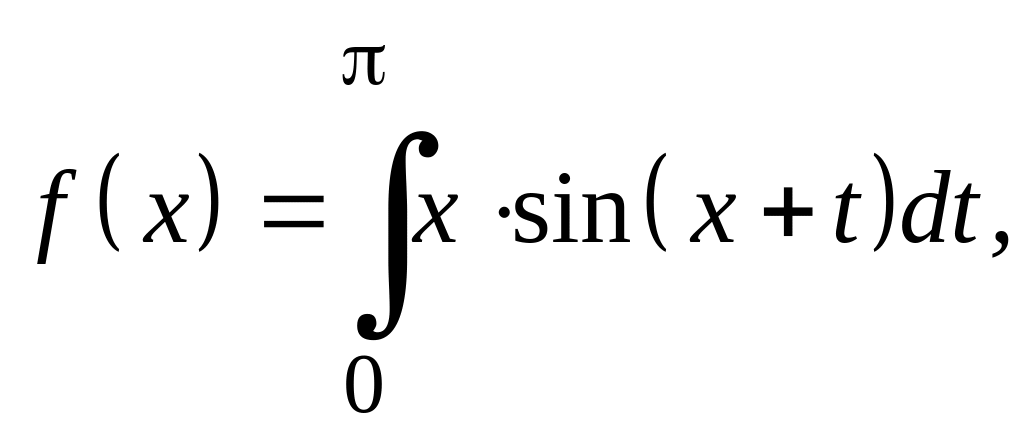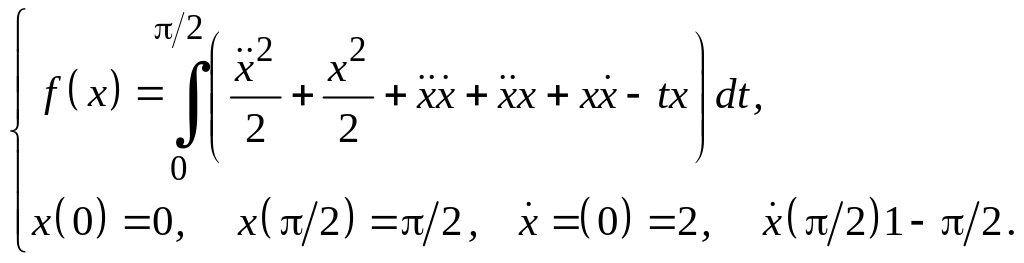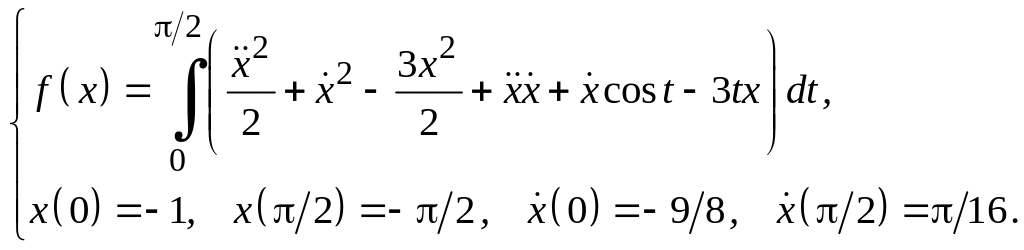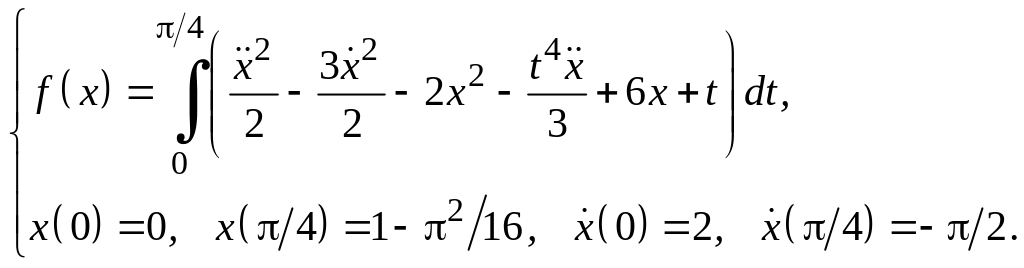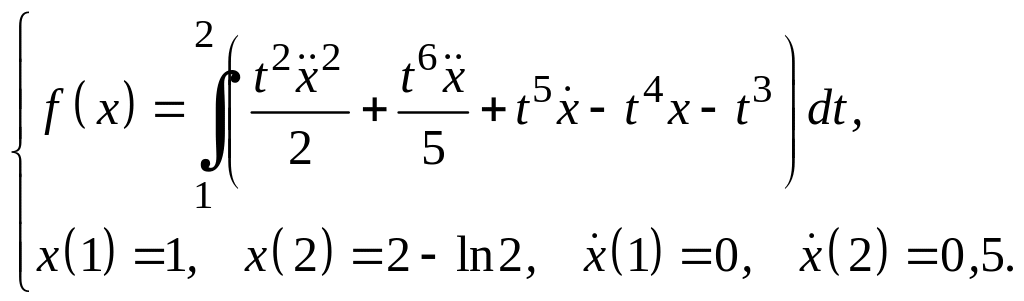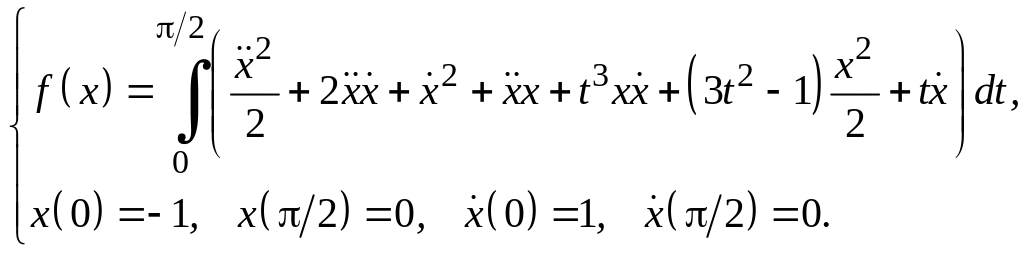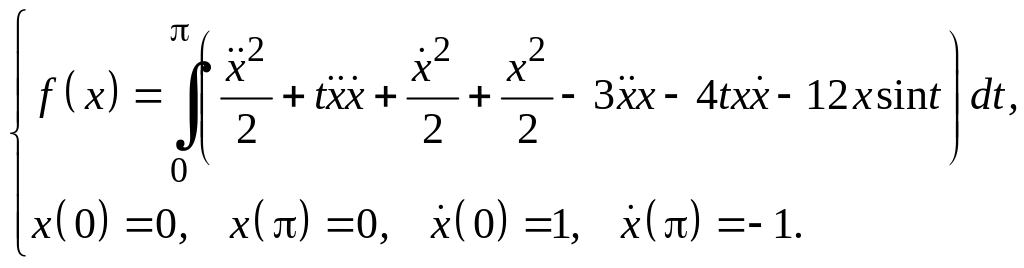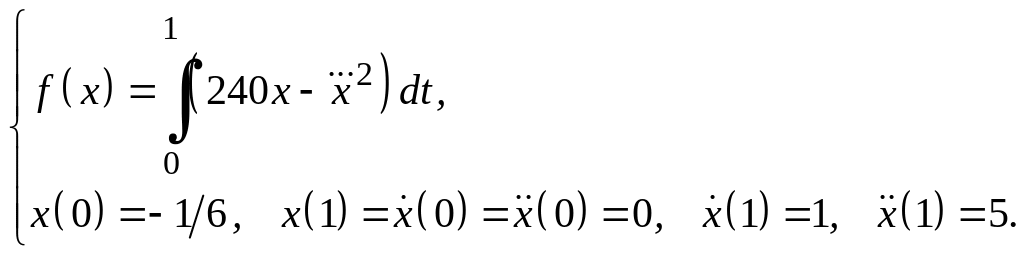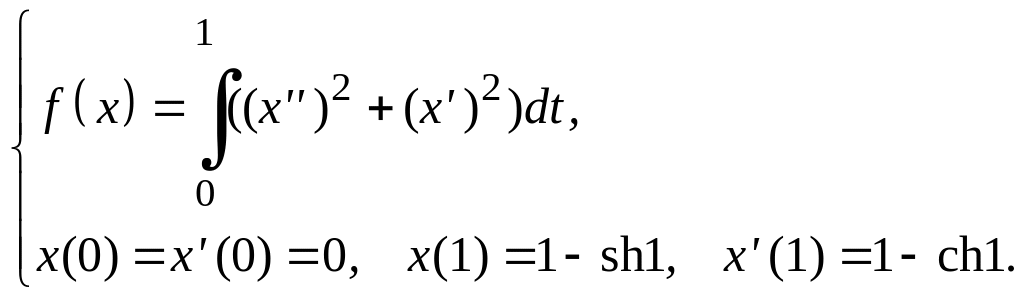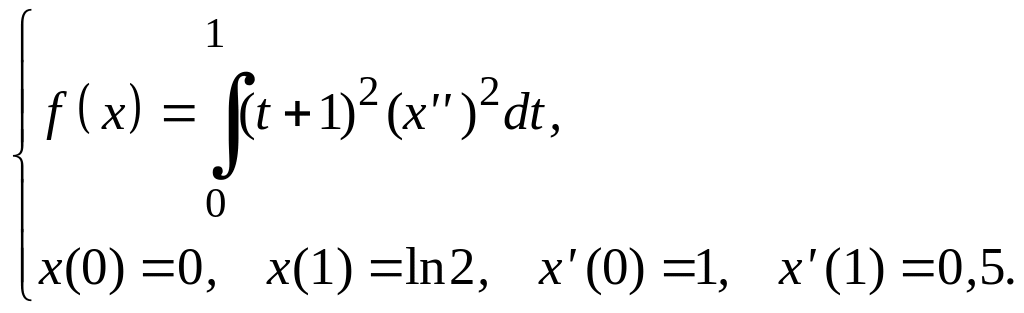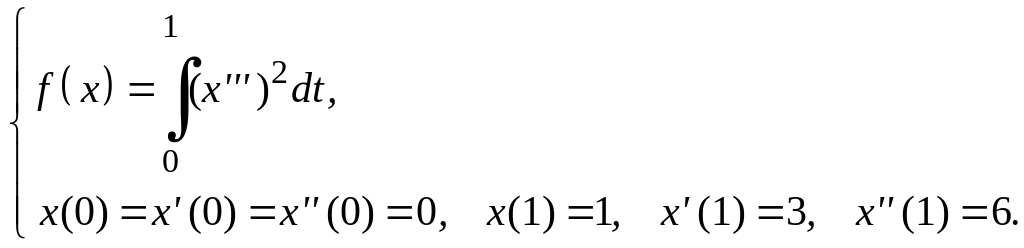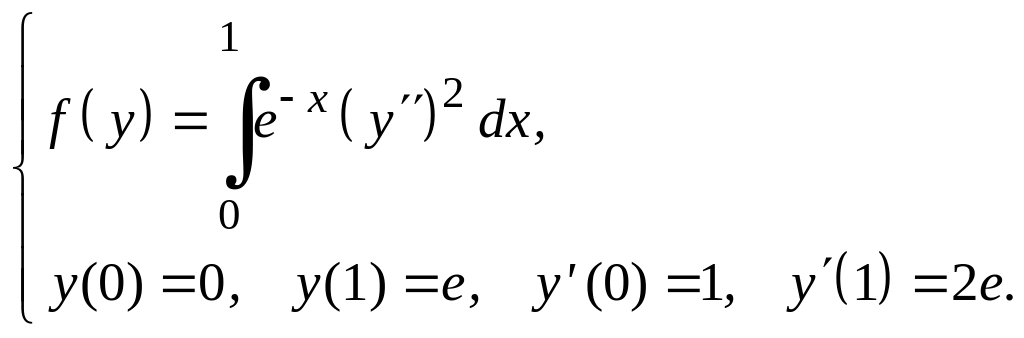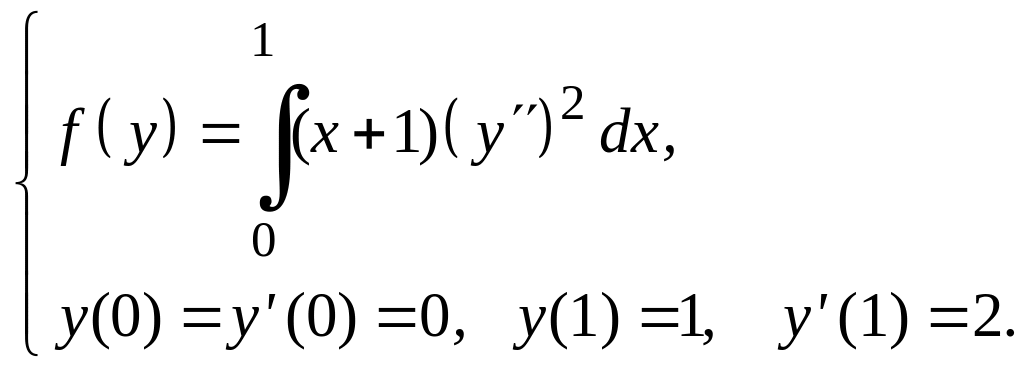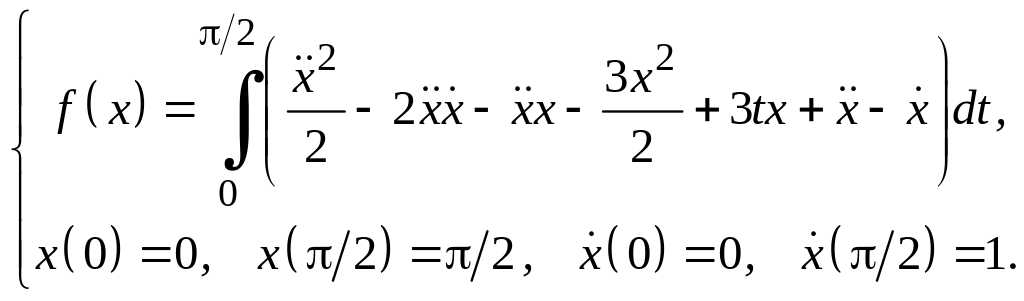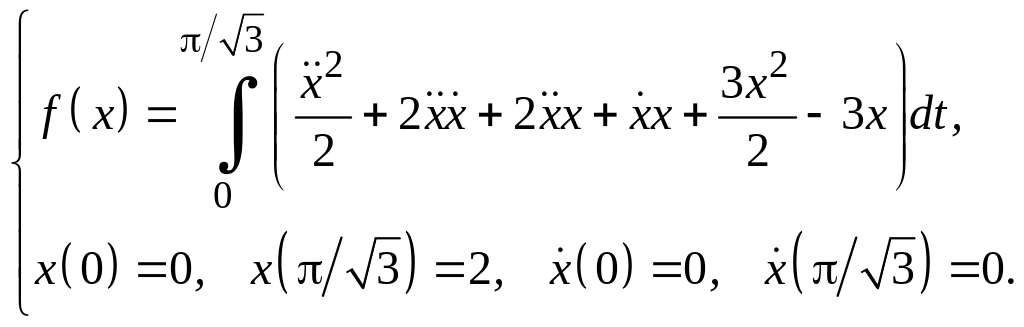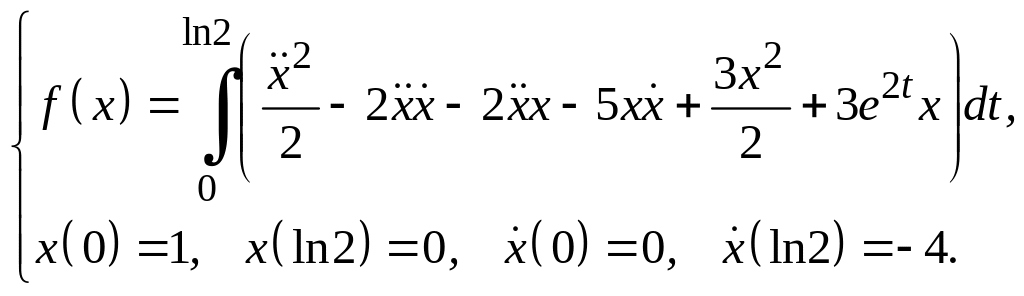Обобщения уравнения Эйлера
Пользуясь теми же методами, несложно получать аналоги уравнений Эйлера для функционалов более общего вида. Остановимся на двух из них.
Для функционалов вида
экстремали являются решениями уравнения Эйлера – Пуассона:
.
Понятно, что для однозначного выбора экстремали требуется дополнительно задать условия на границах:
Для функционалов вида
экстремали являются решениями системы уравнений Эйлера:
.
Соответственно, граничные условия принимают вид:
Пример 4. Найти экстремали следующего функционала
,
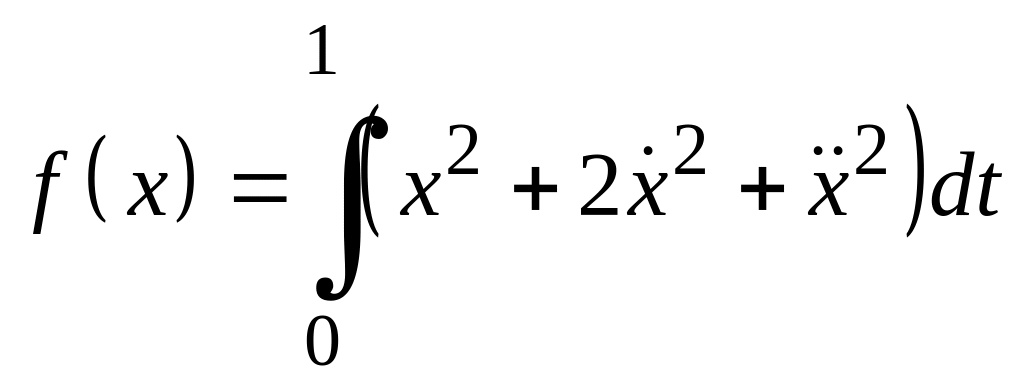удовлетворяющие
условиям:
.
Решение. Уравнение Эйлера – Пуассона имеет вид:
или
.
Решая это уравнение, получаем семейство
экстремалей вида:
.
Учитывая граничные условия, находим
единственную экстремаль
.
Список рекомендуемой литературы
Эльсгольц Л.Э. Дифференциальные ураванения и вариационное исчисление / М.: Эдиториал УРСС, 2000. – 319 с.
Романко В.К. Курс дифференциальных уравнений и вариационного исчисления / М., СПб.: Физматлит, 2000. – 342 с.
Пантелеев А.В. Вариационное исчисление в примерах и задачах / М.: Изд-во МАИ, 2000. – 227 с.
Варианты заданий Задание 1
Найти экстремали следующих функционалов, удовлетворяющих условиям жесткого закрепления.
Задание 2
Исследовать на разрешимость следующие вариационные задачи (в зависимости от значений параметров) и дать полное описание класса экстремалей, когда задача имеет решение.
Задание 3
Для функционалов, зависящих от производных высших порядков, найти экстремали, удовлетворяющие заданным граничным условиям.
