7 Результаты смешивания веществ. Понятия химического соединения, раствора, дис­персной системы, механической смеси. Растворимость и ее мерз.

8. Напряженное состояние покоящейся жидкости.

В неподвижной жидкости возможен лишь один вид напряжения - напряжение сжа­тия. Как отмечалось ранее, жидкость в общем случае может находиться под действием двух сил - силы давления равномерно распределённой по всей внешней поверхности вы­деленного жидкого тела и массовых сил, определяемых характером переносного движе­ния. Под внешней границей жидкого тела могут пониматься как соседние тела: твёрдые (стенки сосуда или трубы, в которые помещена жидкость), газообразные (поверхность раздела между жидкостью и газовой средой), так и условные поверхности, мысленно вы­деляемые внутри самой жидкости. Действующее на внешнюю поверхность жидкости дав­ление обладает двумя основными свойствами: _t

1. Давление всегда направлено по внутренней нормали к выделенной поверхности. Это свойство вытекает из самой сущности давления и доказательств не требует. Тем не менее, поясним этот постулат простым примером. Отсечём от жидкого тела часть его объёма и для сохранения равновесия оставшейся части жидкости приложим к образовав­шемуся сечению систему распределённых сил. По своей вели­чине и напрвлению действия эти силы должны обеспечить эк­ вивалентное влияние на оставшийся объём жидкости со сторо­ны отсечённой части жидкого тела. Поскольку в покоящейся жидкости не могут существовать касательные напряжения, то приложенные к сечению силы могут быть направлены лишь по внутренней нормали к площади сечения.

2. В любой точке внутри жидкости давление по всем направлениям одинаково. Дру­гими словами величина давления в точке не зависит от ориентации площадки, на которую действует давление.

8. Гидростатическое давление и его виды. Поле давления. Поверхность равного дав­ления и плоскость уровня.

Гидростатическое давление

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.

Если эту силу P разделить на площадь дна S_abcd, то мы получим среднее гидростатическое давление, действующее на дно резервуара.

Гидростатическое давление обладает свойствами.

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Свойство 2. Гидростатическое давление неизменно во всех направлениях.

Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Согласно закону внутреннего трения Ньютона, в неподвижной жидкости касательные напряжения  равны 0, так как dV = 0. Растягивающие нормальные напряжения, даже самые незначительные, приводят жидкость в движение, поэтому в неподвижной жидкости они тоже отсутствуют. Таким образом, в неподвижной жидкости действуют только нормальные сжимающие поверхностные (гидростатическое давление) и массовые силы.

Гидростатическое давление обладает двумя свойствами:

– оно всегда направлено по нормали к площадке, на которую действует (из самого определения давления);

– его величина не зависит от направления, то есть ориентации площадки в жидкости.

Различают давление абсолютное, избыточное и давление вакуума. Абсолютным дав­лением называется давление в точке измерения, отсчитанное от нуля. Если за уровень от­счёта принята величина атмосферного давления, то разница между абсолютным давлени­ем и атмосферным называется избыточным давлением.

Если давление, измеряемое в точке ниже величины атмосферного давления, то раз­ница между замеренным давлением и атмосферным называется давлением вакуума

Избыточное давление в жидкостях измеряется манометрами. Это весьма обширный набор измерительных приборов различной конструкции и различного исполнения. 2.2. Свойства гидростатического давления

10. Сжимаемость жидкостей и газов. Коэффициент объемного сжатия и модуль объ­емной' упругости. Закон Гука. Закон Бойля-Мариогга. Бароклннная и баротропная жидкость.

Оценка упругих свойств жидкостей может осуществляться по ряду специальных па­раметров.

коэффициент объёмного сжатия жидкости представляет собой относительное изменение объёма жидкости при изменении давления на единицу. По суще­ству это известный закон Гука для модели объёмного сжатия:

начальный объём жидкости, (при начальном давлении),

коэффициент объёмного (упругого) сжатия жидкости.

Считается, что коэффициент объёмного сжатия жидкости зависит с достаточно большой точностью только от свойств самой жидкости и не зависит от внешних условий. Коэффициент объёмного сжатия жидкости имеет размерность обратную размерности дав­ления, т.е. м/н.

адиабатический модуль упругости жидкости К, зависящий от термодинами­ческого состояния жидкости (величина обратная коэффициенту объёмного сжатия жидкости): ,

Величина модуля упругости жидкости имеет размерность напряжения, т.е. н/м .

закон Бойля-Мариотта, согласно которому при постоянной температуре произведение давления газа на его объем есть величина постоянная.

Закон Бойля-Мариотта гласит: при постоянной температуреимассеидеального газапроизведение егодавленияиобъёмапостоянно:

, где:

p — давление газа

V — объём газа

сжимаемая жидкость — жидкость, плотность которой является переменной величиной и в общем случае зависит от температуры и давления. Соотношение, связывающее между собой давление p, температуру T и }} (или удельный объём), называют уравнением состояния.плотность {{ Для С. ж. (в отличие от несжимаемой жидкости) скорость распространения малых возмущений имеет конечное значение (равное скорости звука), с чем связаны многие особенности обтекания тел потоком С. ж. Наиболее простой моделью С. ж. является баротропная среда, плотность }}(p). Если}} = {{которой есть функция только давления, то есть {{ }}(p) = Cpn, где C и n — некоторые постоянные, то движение таких{{ сред называют политропическим, а величина 1/n — показателем политропы. Случай n = 0 соответствует несжимаемой жидкости, а при n = 1 имеет место изотермическое течение. С. ж., плотность которой не есть функция только одного давления, называется бароклинной. Наиболее распространённой моделью бароклинной жидкости является совершенный газ, }}RT, где R — газоваяудовлетворяющий уравнению Клапейрона p = {{ постоянная, и имеющий постоянные удельные теплоёмкости при постоянном давлении cp и постоянном объёме cV. Область её применимости ограничена }}относительно небольшими температурами движущейся среды (T {{ К). При больших сверхзвуковых скоростях полёта начинают1000 проявляться реального газа эффекты, и необходимо пользоваться различными моделями несовершенного газа.

10. Парообразование и конденсация. Парциальное давление. Давление насыщенного пара.

Испаряемость. Испаряемость присуща всем жидкостям, но в различной степени, причем она сильно зависит от условий, в которых находится жидкость. Одной из характеристик испаряемости является температура кипения при нормальном атмосферном давлении. Но атмосферное давление – это лишь частный случай давления в гидросистеме, поэтому более полной характеристикой испаряемости является давление (упругость) насыщенных паров p_н.п.. Чем выше p_н.п, тем более летучая жидкость. С ростом температуры оно возрастает, но для разных жидкостей в различной степени. Поэтому даже сухой воздух в квартире зимой при контакте с предметом, занесенным с мороза, при остывании становится влажным, и из него конденсируются капельки воды. Это хорошо знают люди, носящие очки. Образование конденсата можно наблюдать на поверхности труб, по которым подается холодная вода, на оконных стеклах и т.п.

Для многокомпонентных жидкостей (смесей) давление насыщенных паров зависит еще и от соотношения объемов паровой и жидкой фаз. Для них давление насыщенных паров тем больше, чем большая доля объема занята жидкостью. В справочниках для них приводятся значения p_н.п. при соотношении объемов паровой и жидкой фаз 4:1.

12. Тепловое расширение жидкостей и газов. Коэффициент теплового расширения. Закон Гей-Люссака. Абсолютный ноль температуры.

Как правило, жидкости и газы расширяются с повышением температуры, а плотность их при этом уменьшается. Исключение составляет вода, плотность которой возрастает при повышении температуры от 0 до 4 °С и достигает максимума при 4 °С. Такая аномалия объясняется особенностями молекулярного строения воды.

Температурное расширение. Температурное расширение – это свойство жидкости изменять свой объем при изменении температуры. Характеризуется коэффициентом температурного расширения _T [1/град], который представляет собой относительное изменение объема, приходящееся на 1 градус:

Для воды коэффициент при увеличении температуры возрастает (приp = 0,1 МПа и изменении температуры от 0 до 100С приблизительно от – 0,000025 до +0,000720). Рост давления при низких температурах приводит к увеличению , а при температурах выше 50С – к его снижению. Для большинства других капельных жидкостей с ростом давления уменьшается.

В конечной форме при _T = const (при малом изменении температуры)

;,

где T = T – T₀ – изменение температуры жидкости.

Изменение объема при нагревании жидкостей весьма ощутимо, поэтому его необходимо учитывать при проектировании гидравлических устройств, в которых жидкость существенно нагревается.

Закон Гей-Люссака может быть записан в виде:

V=V0aT,

 где Т - абсолютная температура, выраженная в К (Кельвинах);

V0 - объем газа при Т = 273 К.

 Очевидно, закон Гей-Люссака неприменим вблизи абсолютного нуля температуры.

Поскольку закон Гей-Люссака справедлив для идеальных газов, реальные газы подчиняются ему в достаточно разреженном равновесном состоянии, когда давление и температура далеки от критических значений, при которых начинается cжижение.Закон был опубликован в 1802 г. Жозефом Луи Гей-Люссаком (1778-1850). При этом Гей-Люссак настоял на том, чтобы он носил имя Жака Александра Цезара Шарля (1746-1823), который открыл этот закон в 1787 году, но не опубликовал его.

Абсолю́тный ноль температу́ры— это минимальный пределтемпературы, которую может иметь физическое тело. Абсолютный ноль служит началом отсчётаабсолютной температурной шкалы, например, шкалыКельвина. По шкалеЦельсияабсолютному нулю соответствует температура −273,15 °C.Считается, что абсолютный ноль на практике недостижим. Его существование и положение на температурной шкале следует изэкстраполяциинаблюдаемых физических явлений, при этом такая экстраполяция показывает, что при абсолютном нулеэнергиятеплового движения молекул и атомов вещества должна быть равна нулю, то естьхаотическоедвижение частиц прекращается, и они образуют упорядоченную структуру, занимая чёткое положение в узлахкристаллической решётки. Однако, на самом деле, даже при абсолютном нуле температуры регулярные движения составляющих вещество частиц останутся^[1]. Оставшиеся колебания, напримернулевые колебания, обусловлены квантовыми свойствами частиц ифизического вакуума, их окружающего.^[1]В настоящее время в физических лабораториях удалось получить температуру, превышающую абсолютный ноль всего на несколько миллионных долей градуса; достичь же его самого, согласно законам термодинамики, невозможно.

12. Уравнение Эйлера равновесия жидкости.

Получим дифференциальные уравнения равновесия жидкости в общем случае, когда на нее действуют не только сила тяжести, но и другие массовые силы (сила инерции переносного движения). В неподвижной жидкости возьмем произвольную точку M с координатами x, y и z и давлением p. Система координат жестко связана с сосудом, содержащим жидкость.

Выделим в жидкости элементарный объем в виде прямоугольного параллелепипеда с ребрами, параллельными осям координат и равными dx, dy, dz. Точка M – одна из вершин параллелепипеда (Рис. 3). Рассмотрим условия равновесия этого объема. Пусть внутри его на жидкость действует равнодействующая единичная массовая сила, составляющие которой X, Y, Z. Тогда массовые силы, действующие на выделенный объем в направлении осей, будут равны этим составляющим, умноженным на массу объема жидкости.

Разделим уравнения на массу выделенного объема и перейдем к пределу, устремив dx, dy и dz к 0. Тогда в пределе получим условия равновесия жидкости в точке M (уравнения Эйлера):

На практике вместо системы уравнений удобнее одно эквивалентное уравнение, не содержащее частных производных. Домножим уравнения Эйлера соответственно на dx, dy и dz и сложим их.

Последнее уравнение выражает изменение давления при изменении координат точки.

Рассмотрим частный случай. Пусть из массовых сил действует только сила тяжести. Тогда X = Y = 0, а Z = – g. Тогда полученное уравнение примет вид:

Проинтегрируем уравнение

Константу интегрирования найдем из граничного условия на свободной поверхности:

Тогда

Мы получили основное уравнение гидростатики.

12. Уравнение состояния вещества. Уравнение Клапейрона. Уравнение Клапейрона-Менделеева.

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением,молярным объёмомиабсолютной температуройидеального газа. Уравнение имеет вид:

где

— давление,

— молярный объём,

— абсолютная температура,

—универсальная газовая постоянная.

Плотность идеальных газов при давлениях отличных от атмосферного можно опре­делить по известному закону газового состояния Менделеева-Клайперона:

12. Барометрическая формула. Основной закон гидростатики для несжимаемой жид­кости: его энергетическая и геометрическая интерпретация.

Основное уравнение гидростатики

Рассмотрим случай равновесия жидкости в состоя­нии «абсолютного покоя», т.е. когда на жидкость дейст­вует только сила тяжести. Поскольку объём жидкости в сосуде мал по сравнению с объёмом Земли, то уровень свободной поверхности жидкости в сосуде можно счи­тать горизонтальной плоскостью. Давление на свобод­ную поверхность жидкости равно атмосферному давле­ниюр₀. Определим давление р в произвольно выбран­ной точке М, расположенной на глубине h. Выделим

около точки М горизонтальную площадку площадью dS . Построим на данной площадке вертикальное тело, ограниченное снизу самой площадкой, а сверху (в плоскости свобод­ной поверхности жидкости) её проекцией. Рассмотрим равновесие полученного жидкого тела. Давление на основание выделенного объёма будет внешним по отношению к жид­кому телу и будет направлено вертикально вверх. Запишем уравнение равновесия в про­екции на вертикальную ось тела.

Сократив все члены уравнения на dS, получим:

Давление во всех точках свободной поверхности одинаково и равно р₀, следова­тельно, давление во всех точках жидкости на глубине h также одинаково согласно основ­ному уравнения гидростатики. Поверхность, давление на которой одинаково, называется поверхностью уровня. В данном случае поверхности уровня являются горизонтальными плоскостями.

Выберем некоторую горизонтальную плоскость сравнения, проходящую на расстоя­нии z₀ от свободной поверхности, тогда можно записать уравнение гидростатики в виде:

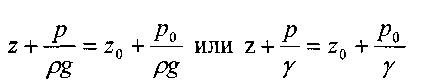
Все члены уравнения имеют линейную размерность и носят название:

z- геометричкская высота,

p/y- пьезометрическая высота

Величинаносит название гидростатического напора.

Основное уравнение гидростатики, доказанное на примере жидкости находящейся под действием только сил тяжести, будет справедливо и для жидкости, которое испытыва­ет на себе ускорение переносного движения. Под действием сил инерции переносного движения будет меняться положение свободной поверхности жидкости и поверхностей равного давления относительно стенок сосуда и относительно горизонтальной плоскости. Вид этих поверхностей целиком зависти от комбинации ускорений переносного движения и ускорения сил тяжести. В литературе состояние равновесия жидкости при наличии пе­реносного движения называется относительным покоем жидкости. Любые комбинации ускорений сводятся к двум возможным видам равновесия жидкости

12. Сила давления жидкости на плоскую стенку. Центр давления. Гидростатический парадокс.