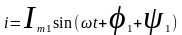27. Электрические цепи несинусоидального тока. Основные понятия.
Периодическими несинусоидальными токами – называются токи, изменяющиеся во времени, но по периодическому несинусоидальному закону.
Генераторы таких напряжений называются релаксационными. Используются в различных устройствах импульсной техники.
Несинусоидальные токи возникают при 4 режимах работы:
Источник электрической энергии вырабатывает несинусоидальную ЭДС и несинусоидальный ток, все элементы электрической цепи линейны (от величины тока не зависят).
Источник электрической энергии вырабатывает синусоидальную ЭДС и синусоидальный ток, но один или несколько элементов электрической цепи – нелинейны (имеют нелинейную ВАХ).
Источник электрической энергии вырабатывает нелинейную ЭДС и нелинейный ток, все элементы нелинейны.
Источник электрической энергии вырабатывает синусоидальную ЭДС и синусоидальный ток, но один или несколько элементов электрической цепи, в процессе работы, меняют свои характеристики (вариканы у емкости).
Несинусоидальные колебания могут быть периодическими и непериодическими. При рассмотрении периодических несинусоидальных колебаний, можно воспользоваться теоремой Фурье, согласно которой, любая периодически изменяющаяся величина, может быть представлена в виде суммы постоянной составляющей и синусоидальных колебаний с кратной частотой.
Гармоники - синусоидальные составляющие несинусоидального колебания.
Синусоидальная составляющая, частота которой совпадает и равна частоте несинусоидального колебания, называется главной или основной гармоникой.
Синусоидальные составляющие, частоты которых в 2, 3 и n-раз больше частоты несинусоидального колебания, называются высшими гармониками.
В общем случае:
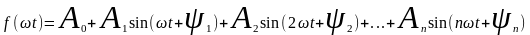
А0 – постоянная составляющая.
А1, А2...Аn – амплитуда соответствующих гармоник
1, 2…n – частота гармоник
Ѱ1, Ѱ2, Ѱn – начальные фазы гармоник
Гармоники 1, 3, 5, 7 и т.д. – нечетные.
Гармоники 2, 4, 6, 8 и т.д. – четные.
С увеличением частоты гармоники, амплитуда гармоники уменьшается. Чем больше номер гармоники, тем меньше амплитуда.
30. Расчет линейных цепей несинусоидального тока.
Рассмотрим расчет линейных электрических цепей, находящихся под нелинейным напряжением. Допустим, что к цепи, состоящей и? R, L, и С приложено несинусоидальное напряжение, которое изменяется по следующему закону:
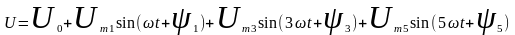
Произведем замену приложенного данного несинусоидального напряжения, последовательно соединенными источниками.
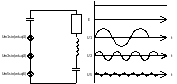
Расчет сопротивлений для различных составляющих несинусоидального тока.
Если пренебречь поверхностным эффектом, будем считать, что величина R на всех гармониках будет одинаковой и будет равна R.
Индуктивное сопротивление:
XL=ω1L
XLK=kω1L=kXL1
XCK=1/kω1c=XC1/k
K – номер гармоники
Для постоянной составляющей А0, U0 Xc=1/0=Ꝏ
Определяем полное сопротивление цепи для каждой гармоники:
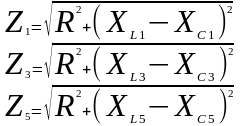
Определение действующих значений несинусоидального тока и напряжения (показания приборов)
Токи:
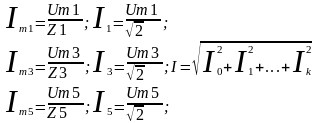
Напряжения:
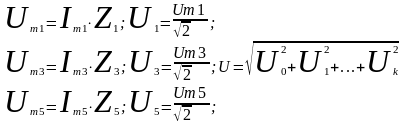
Определение углов сдвига между током и напряжением на каждой гармонике:
Записываем выражение изменения тока от заданного выражения приложенного напряжения
