46. Разветвленная rlc цепь.

Если к источнику синусоидального напряжения подключить катушку индуктивности и

конденсатор параллельно, то токи в ветвях будут протекать следующим образом:

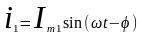
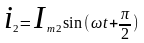
Построим векторную диаграмму токов и напряжений:

Из диаграммы видно, что обычный ток i будет равен i=I_msin(ωt±ϕ).

Знак «-», перед начальной фазой, означает, что характер цепи – индуктивный.

Знак «+», перед начальной фазой, означает, что характер цепи – емкостной.

Если знак не тот и не другой, то ϕ отсутствует.

47. Резонанс токов.

Резонанс токов наступает в цепи синусоидального тока с параллельным соединением катушки индуктивности и конденсатора, при равенстве реактивных проводимостей: b_L=b_C Особенности цепи при резонансе:

1. Полная проводимость равна активной проводимости

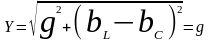
2. Результирующий ток при резонансе токов

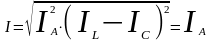- min

3. Полная мощность при резонансе токов

4. Коэффициент мощности при резонансе токов

ϕ=0; cosϕ=1

48. Коэффициент мощности и его значение.

Чем меньше cosϕ – тем больше ток потребителя. Это значит, что больший ток проходит по ЛЭП, а соответственно больше потери линии, меньше КПД линии и всей энергосистемы в целом.

Кроме того, увеличение тока – требует увеличивать диаметр провода, а с ними и затраты. Поэтому каждая организация борется за коэффициент мощности, им небезразлично, как расходуется энергия. На таких предприятиях коэффициент мощности является важным показателем.

Второй семестр

1. Формы записи комплексного числа. Действия над комплексными числами.

Существует три формы записи комплексного числа:

1. Алгебраическая: c=a+jb

2. Тригонометрическая: c=|c|cosϕ+j|c|sinϕ

3. Показательная: с=|c|e^jϕ

Для перевода комплекса из показательной формы в алгебраическую, необходимо, вначале перейти в тригонометрическую форму, а затем в алгебраическую, а из алгебраической формы можно сразу переходить к показательной, найдя модуль и аргумент.

Комплексы можно складывать, вычитать, умножать и делить.

Сложение и вычитание производится только в алгебраической форме.

При сложении: складывают отдельно действительные и мнимые числа:

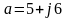
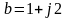
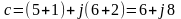
При вычитании из действительной части первого числа - вычитаем действительную часть второго, а из мнимой первого числа - мнимую второго числа.

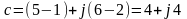
Если одно число в алгебраической форме, а другое в показательной, то нужно второе перевести в алгебраическую для сложения или вычитания.

Умножение и деление производится в алгебраической и показательной форме.

Алгебраическая форма:

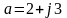
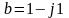
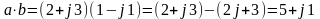
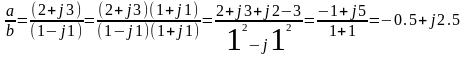
Показательная форма:

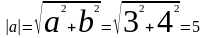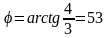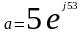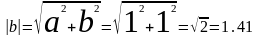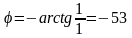; ^о; ;

; ^о; ;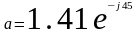

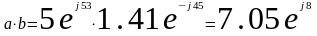
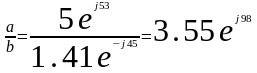
i=I_msin(ωt+ϕ)

Модуль – действующее значение тока.

Аргумент – начальная фаза.

2. Комплексы тока, напряжения, мощности, сопротивления и проводимости.

Если ток и напряжение и ЭДС изменяются синусоидально, то их можно изобразить вектором, а значит записать в комплексном виде.

Точка над комплексом означает, что величина изменяется синусоидально.

Модулем является - действующее значение переменной величины.

Аргументом – начальная фаза.

Комплекс полного сопротивления цепи – определяется отношением комплекса напряжений к комплексу тока. Комплекс полного сопротивления не является синусоидальной величиной, а потому подчеркивается.

Модулем является – полное сопротивление цепи.

Аргументом – угол сдвига фаз, между током и напряжением.

Вещественное число комплекса – R, мнимое – X.

Комплекс проводимости – обратная величина комплекса сопротивлений.

Комплекс мощностей – произведение комплекса напряжений и сопряженного комплекса тока.

При комплексном сопряжении меняем знак «йот» (j) в степени показательной степени.

Модулем является – полная мощность.

Аргументом – угол сдвига фаз, между током и напряжением.

Вещественное число комплекса – P, мнимое – Q.

Если перед мнимым числом стоит «+» - характер цепи – индуктивный.

Если перед мнимым числом стоит «-» - характер цепи – емкостной.