Первый семестр

36. Особенности цепей переменного тока. Переменный ток в цепи с активным сопротивлением.

Активным сопротивлением (Ra) обладают элементы, которые, при прохождении через них тока, нагреваются (лампы накаливания, обогреватели).

Если в цепи присутствует элемент с активным сопротивлением, то к клеммам приложено напряжение u=U_msinωt. В результате данного напряжения протекает ток по закону Ома: .

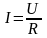Цепи, с активным сопротивлением, будет соответствовать закон Ома для действующих значений.

Действующее значение силы тока, прямо пропорционально действующему значению, приложенного напряжения и обратно пропорционально активному сопротивлению. .

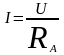Следовательно, закон Ома, для цепи переменного тока, с активным сопротивлением, может быть записан для мгновенных, амплитудных и действующих значений тока и напряжения.

Ток и напряжение изменяются по синусоидальному закону и совпадают по фазе друг с другом.

Активная мощность (P) – средняя мощность цепи. Она определяет скорость необратимого процесса преобразования электрической энергии в другие виды энергии.

37. Цепь переменного тока с индуктивностью.

Идеальная индуктивность (L) – индуктивность, элемента цепи сопротивлений, которой можно пренебречь.

Если в цепи присутствует элемент с идеальной индуктивностью, то в ней протекает переменный ток i=I_msinωt. Он создаст переменный магнитный поток ф=Ф_msinωt, который индуцирует ЭДС самоиндукции.

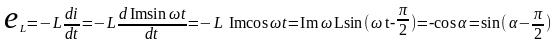
Таким образом, ЭДС самоиндукции (e_L), цепи с идеальной индуктивностью, а также ток, вызвавший ее, изменяется по синусоидальному закону, но отстает от тока на 90^О на векторной и разветвленной диаграмме. Когда ток достигает максимума, скорость его изменения равна нулю I=0. Значит, ЭДС тоже равна нулю, в моменты времени, когда скорость изменения тока максимальная. Соответственно, напряжение изменяется, достигая максимума. Значит направление ЭДС определено по синусу.

Таким образом, U приложенное к цепи с идеальной индуктивностью, как и ток в этой цепи, изменяется по синусоидальному закону и опережает ток на участке ЭДС, на 90^О_. Приложенное напряжение к цепи, вызывает в ней такой ток, который при своем изменении в каждый момент времени, индуцирует равную по амплитуде, но противоположную по знаку ЭДС, относительно приложенного напряжения. E_m=I_mωL

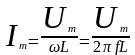
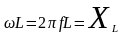
X_L – это индуктивное сопротивление, то есть противодействие переменному току, которое оказывает ЭДС самоиндукции.

Цепи, с индуктивным сопротивлением, будет соответствовать закон Ома для действующих значений.

Действующее значение силы тока, прямо пропорционально действующему значению, приложенного напряжения и обратно пропорционально индуктивному сопротивлению. .

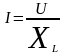Формула мгновенной мощности в цепи с индуктивностью:

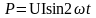
Из формулы видно, что мгновенная мощность в цепи синусоидального тока с идеальной индуктивностью, изменяется по синусоидальному закону. Следовательно, среднее значение этой мощности за период равна нулю.

Реактивная мощность (QL) в цепи с идеальной индуктивностью - та мощность, которая колеблется между источником и магнитным полем индуктивности, которой обмениваются цепь переменного тока и источник питания.

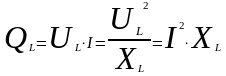
38. Цепь переменного тока с емкостью.

Если, конденсатор с емкостью находится под напряжением u=Umsinωt, то заряд Q=CU, изменяется пропорционально напряжению.

Если увеличивается напряжение, значит увеличивается заряд на конденсаторе, то есть конденсатор заряжается и в цепи возникает зарядный ток.

Если уменьшается напряжение, значит уменьшается заряд на конденсаторе, то есть конденсатор разряжается и в цепи возникает разрядный ток.

Следовательно, при приложенном переменном напряжении, конденсатор периодически заряжается и разряжается. В цепи возникает переменный ток, равный скорости изменения заряда на обкладках конденсатора.

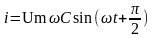
Из формулы видно, что ток и напряжение, в цепи с емкостью, изменяется по синусоидальному закону, но напряжение отстает от тока на 90О.

Цепи, с индуктивным сопротивлением, будет соответствовать закон Ома для действующих значений.

Действующее значение силы тока, прямо пропорционально действующему значению, приложенного напряжения и обратно пропорционально емкостному сопротивлению. .

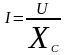Емкостное сопротивление (X_C) – это противодействие, которое оказывает напряжение заряженного конденсатора, приложенному, к этому конденсатору, напряжению.

Мощность цепи с емкостью, изменяется по синусоидальному закону с двойной частотой, следовательно, активная мощность цепи с емкостью, равная среднему значению мгновенной мощности, за период, равна нулю.

Реактивная мощность (QС) в цепи с емкостью - та мощность, которая колеблется между источником и конденсатором.

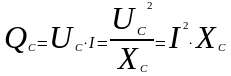
39. Цепь переменного тока с активно-индуктивной нагрузкой. Если по цепи, с активным сопротивлением и индуктивностью или по реальной катушке индуктивности, протекает переменный ток i=Imsinωt, он создает падения напряжения на активном сопротивлении и на индуктивном сопротивлении.

Напряжение на активном сопротивлении – синусоидальное и совпадает по фазе с током. Напряжение на индуктивном сопротивлении – синусоидальное и опережает ток на 90О.

Чтобы понять эти отношения построим векторную диаграмму. Соединим начало вектора Ua с концом вектора UL. Получим вектор U, общего напряжения, приложенного к цепи. Угол ϕ показывает сдвиг между током и напряжением данной цепи. Получим треугольник напряжений.

Цепи, с активным сопротивлением и индуктивностью, будет соответствовать закон Ома для действующих значений.

Действующее значение силы тока, прямо пропорционально действующему значению, приложенного напряжения и обратно пропорционально полному сопротивлению цепи c активным сопротивлением и индуктивностью. .

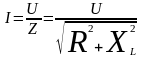Если стороны треугольника напряжений поделить на ток – получим треугольник сопротивлений, у которого катеты – активное и реактивное сопротивление, гипотенуза – полное сопротивление.

Если стороны треугольника напряжений умножить на ток – получим треугольник мощностей, у которого катеты – активная и реактивная мощность, гипотенуза – полная мощность.

40. Цепь переменного тока с активно-емкостной нагрузкой. Если по цепи, с активным сопротивлением и емкостью протекает переменный ток i=I_msinωt, он создаст падения напряжения на активном сопротивлении и на конденсаторе.

Построим векторную диаграмму. Соединим конец вектора U_C с началом вектора U_A. Получим вектор U, общего напряжения, приложенного к цепи. Оно синусоидально и отстает от тока на ϕ.

Получим треугольник напряжений.

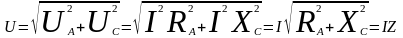
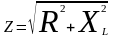- полное сопротивление цепи

Цепи, с активным сопротивлением и емкостью, будет соответствовать закон Ома для действующих значений.

Действующее значение силы тока, прямо пропорционально действующему значению, приложенного напряжения и обратно пропорционально полному сопротивлению цепи c активным сопротивлением и емкостью. .

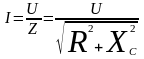Если стороны треугольника напряжений поделить на ток – получим треугольник сопротивлений, у которого катеты – активное и реактивное сопротивление, гипотенуза – полное сопротивление.

Если стороны треугольника напряжений умножить на ток – получим треугольник мощностей, у которого катеты – активная и реактивная мощность, гипотенуза – полная мощность.