- •Нижегородский государственный
- •Иерархическое соподчинение то
- •Классификация деятельности
- •Инженерная деятельность Ее место и отношение с рабочими видами деятельности
- •Направления инженерной деятельности
- •Направление проектирования
- •Основные требования к проекту
- •Процесс конструирования.
- •Системный подход
- •Структура и иерархия
- •Регулирование в системе
- •Иерархия
- •Принцип неопределенности
- •Исследование действий и решений
- •Единицы измерения физических величин. Подобие и метод размерности.
- •Метод размерностей
- •Техническое регулирование и его роль в инженерной деятельности
- •Основные понятия
- •Принципы технического регулирования
- •Принятие технических регламентов
Единицы измерения физических величин. Подобие и метод размерности.
Метрология – это наука об измерениях физических величин, способах обеспечения единства и требуемой точности измерений.
Существуют 2 способа измерения физических величин:
1 – непосредственное измерение
2 – косвенное измерение.
Единицы физических величин:
будем использовать международную систему измерений Си.
В основу любых систем измерений физических величин положен принцип min количества основных единиц измерений.
Основные единицы измерения:
- единицы длины (м);
- единицы массы (кг);
- единицы времени (с);
- единицы силы электрического тока (А);
- единицы термодинамической температуры (К);
- единицы количества вещества (моль);
- единицы силы света (Кандел).
Дополнительные единицы измерения:
- плоского угла (рад);
- телесного угла (стер).
Размерностью любой физической величины называется ее выражение через символы основных системных единиц:
L – символ длины;
M – символ массы;
T – символ времени;
I – символ электрического тока;
θ – символ термодинамической температуры;
– символ термодинамической температуры;
N – символ количества вещества;
![]() - символ
единицы света.
- символ
единицы света.
В общем виде размерность физической величины можно записать в виде формулы:
![]()
[ ] – показывают, что рассматривается размерность физической величины.
Если мы запишем [l], то запись будет выглядеть следующим образом:
![]()
Теорема 1:
Если численное значение величины С равно произведению численных величин А и В, то размерность С равна произведению размерностей А и В.
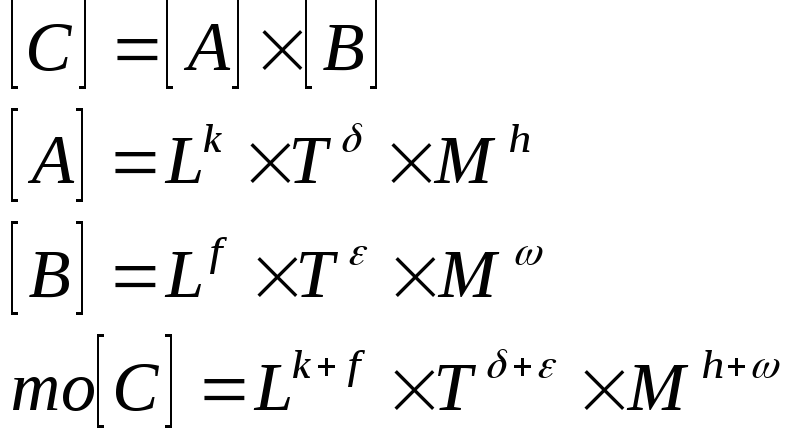
Теорема 2:
Если численное значение величин С равно отношению численных значений величин А и В, то размерность С равна отношению размерностей А и В.
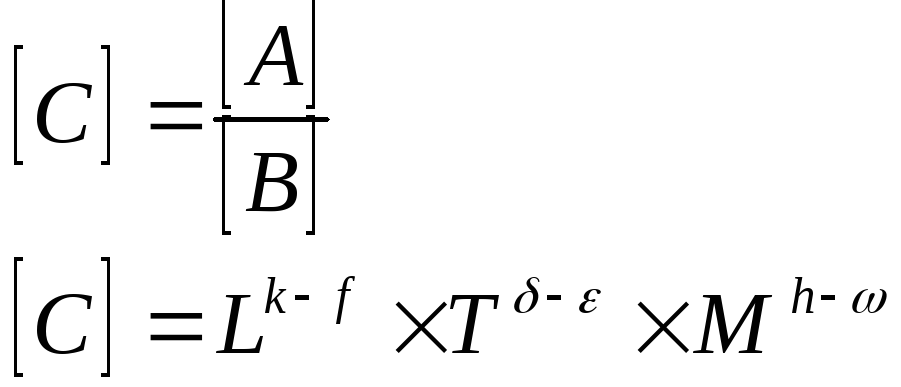
Безразмерные величины играют большую роль в технике.
![]()
Теорема 3:
Если численное значение величины С равно степени n численного значения равно размерности Аn.
![]()
Правило: размерность всех величин, которые входят в правую и левую части уравнения должны быть одинаковы, как бы не были сложны уравнения.
Метод размерностей
Данный метод построен на исполнении формул, теорем и правил размерностей.
«Подобие» - два явления подобны, если по заданным характеристикам одного сложного можно получить характеристику другим простым пересчетом, который аналогичен переходу от одной системы единиц измерения к другой. Для того, чтобы провести пересчет необходимо знать необходимые масштабы.
Численные характеристики для различных, но подобный явлений можно рассматривать как численные характеристики одного и того же явления, но выраженные в двух различных системах измерения.
Для сохранения подобия в моделировании необходимо соблюдать условия, которые на практике не соблюдаются, поэтому возникает вопрос об ошибке или о масштабном эффекте, когда мы переносим результаты, полученные на модели, на натуру.
«Для всякой совокупности подобных явлений все безразмерные характеристики имеют одинаковые численные значения», - Седов.
 Справедливо
также обратное утверждение: если все
безразмерные характеристики для двух
явлений одинаковы, то явления подобны.
Справедливо
также обратное утверждение: если все
безразмерные характеристики для двух
явлений одинаковы, то явления подобны.
Теорема Бэкингема: если у нас имеется n основных независимых физических величин, число зависимых величин – к (к>n), то число безразмерных величин будет равно к-n=p.
Безразмерные величины играют большую роль и являются критериями подобия.
Переход к безразмерному виду уменьшает число переменных до числа, определенным данным уравнением: p=k-n.
Примеры.
1.

Определить
период колебания такого маятника. При
этом считается, что маятник совершает
малые колебания.
![]()
Так как отклонения малые, то углом отклонения пренебрегаем.
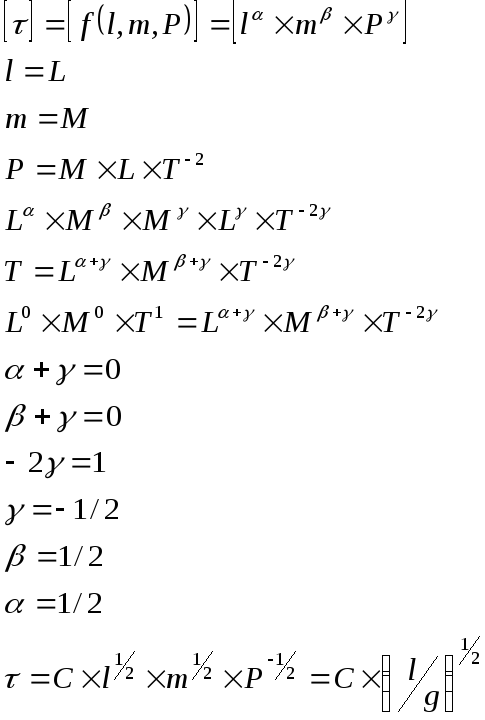
2. Поток идеальной несжимаемой жидкости обтекает шар.
![]()
![]()
 Скорость
потока на входе υ. Принимаем давление
в дали от шара равное 0.
Скорость
потока на входе υ. Принимаем давление
в дали от шара равное 0.
А в центре шара Р=Р0.
Найти зависимость: