9. Классическое определение вероятности. Свойство вероятности.

Числовая характеристика возможности появления случайного события в эксперименте называется вероятностью этого события. Если в некотором смысле вероятности элементарных исходов одинаковы, т.е. элементарные исходы равновозможные, то логично считать, что

в этом случае условия а) и б) выполняются:

, тогда .

9. События зависимые и независимые. Условная вероятность. Теорема умножения вероятностей.

Рассмотрим произвольное вероятностное пространство и два события А и В. Будем считать, что Что можно сказать о вероятности события В, если известно, что произошло событие А? Тот факт, что событие А произошло, несет некоторую дополнительную информацию о пространстве элементарных исходов, что, возможно, изменяет вероятность появления В.По определению вероятность события В, найденная в предположении, что произошло некоторое событие А, называется условной вероятностью события В обозначается

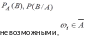
Если событие А произошло, то некоторые из элементарных исходов становятся

, и мы можем рассматривать новое усеченное пространство элементарных

исходов, из которых невозможные исходы исключены, т.е. .Условная вероятность равна:

Вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

9. Основные формулы теории вероятности. Формула полной вероятности.

называются полной группой.

Формула полной вероятности и формула Байеса

Если событие А может произойти только при выполнении одного из событий  , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

.

Эта формула называется формулой полной вероятности.

Вновь рассмотрим полную группу несовместных событий  , вероятности появления которых  . Событие А может произойти только вместе с каким-либо из событий  , которые будем называть гипотезами. Тогда по формуле полной вероятности

Если событие А произошло, то это может изменить вероятности гипотез  .

По теореме умножения вероятностей

,

откуда

.

Аналогично, для остальных гипотез

Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез   называются апостериорными вероятностями, тогда как   - априорными вероятностями.

9. Понятие случайной величины. Определение закона распределения случайной величины.

Случайной величиной-величина, которая при данном осуществлении данного опыта принимает то или иное числовое значение, заранее не известное какое именно. Случайные величины обозначаются Х, Y и т.д. Например, опыт - бросается игральная кость один раз. Случайная величина Х - число выпавших очков. Множество значений случайной величины Х={1,2,3,4,5,6}. Любое правило, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.

9. Законы распределения дискретных случайных величин. Ряд распределения.

Случайная величина называется дискретной, если она принимает конечное или счетное множество значений. Биномиальное распределение-Производится серия испытаний по схеме Бернулли: проводится n независимых опытов, в каждом из которых интересующее нас событие А наступает с одной и той же вероятностью p, – вероятность наступления события в каждом отдельном опыте. Случайная величина X – число наступлений события А в рассматриваемой серии опытов, то есть число «успехов». Распределение Пуассона.