7. Технические допуски в антеннах
Форма
ДН начинает заметно искажаться, а КНД
уменьшатся если ψ ˃
(
/2).
Поэтому разность хода луча из фокуса
до раскрыва, вызванная неточностью
использования антенны в какой-либо ее
части, не должна превышать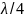
.
Исходя из этого условия устанавливаются технические допуски.
Параболическое зеркало
1
.
Точность изготовления отражателя:
Рис. 13. Рис. 14.
Рисунок 13. Параболическое зеркало с разностью хода 2δ.
Рисунок 14. Параболическое зеркало с разностью хода δ.
ψmax
доп =
/2
2δ ≤
δ ≤
δ = 0,3125
Берут
δдоп = (±(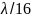
))
= 0,15625
Из рисунка видно, что максимум изменения длинны пути имеет место в центре отражателя, когда путь изменяется на 2δ.
Т.к. отклонение формы поверхности от заданной могут иметь в разных точках противоположные знаки, то за допуск берут величину вдвое меньшую
δдоп = (±( ))
Это
все применимо для искажений с площадкой
.
Допускаемая дефокусировка облучателя
Рис.15. Рис.16.
Если облучатель в фокусе F, то пути равны для центрального луча и кратного.
ᶩ1 = 2 (OF) = ᶩ2 = FD + DK
2f = r0 + r0 cos
При смещении облучателя в точку F', получим
ᶩ1' = 2 (OF) + 2δf = 2f + 2δf
ᶩ2' = F'D + D'K = FD + δf cos ' + DK + δf
ᶩ1'-
ᶩ2'
= 2 (OF) + 2δf
- (FD + DK + δf
+ δf
cos
ᶩ1'-
ᶩ2'
= δf
(1-cos
')
≤ (
δf
≤
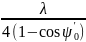
т.к. ' ≈ , т.к. δf ≤ f , то
δf
≤
≤
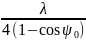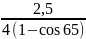≤ 1,08
При
,
берут
δf
≤
, δf
≤ 0,625
Угол отклонения ДН:
=
*
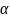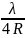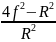= 0,026 (рад)
8. Расчет распределения поля в раскрыве зеркала и аппроксимирующих функций
По
формуле Ems
= cos2
fобл()
производится расчет поля в раскрыве
[1, с.14]. Далее подбирают теоретическую
аппроксимирующую функцию [1, с.14]:
Ems
=
+ (1 - )
* [1 – (
)2]p,
где p=1,2,3 – степень аппроксимирующей функции, Δ уровень поля на раскрыве, ρ – координаты на раскрыве зеркала.
Результаты расчетов сведены в табл. 5.
Таблица 5. Истинное поле в раскрыве зеркала
-
0
15
30
45
60
65
Ems
1
0,914
0,757
0,513
0,276
0,219
Результаты расчетов сведены в табл. 6.
Таблица 6. Аппроксимирующие функции
-
r/r0
p=1
p=2
p=3
Ems(истинное)
0
1
1
1
1
0,202
0,96
0,93
0,91
0,91
0,412
0,87
0,76
0,67
0,75
0,637
0,69
0,51
0,4
0,51
0,888
0,4
0,27
0,25
0,27
1
0,2
0,2
0,2
0,2
Графическое изображения аппроксимирующих функций и истинного поля в раскрыве, представлены ниже на рисунке 17.
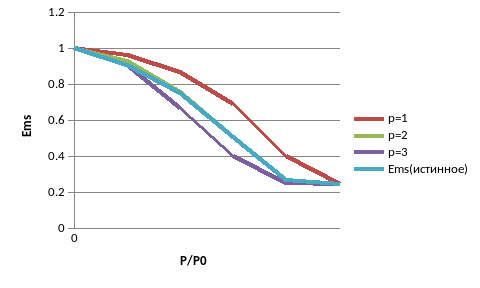
Рисунок 17. Истинное поле в раскрыве и аппроксимирующие функции
Из данного графика видно, что самая близкая к истинному распределению функция со степенью аппроксимации p=2.