14. Изобразите на рисунке уровни энергии атома водорода.

15. Изобразите на рисунке уровни энергии атома водорода. Электрон в атоме водорода переходит с 5-го уровня на 3-ий уровень. В какой области спектра будет находится излучение? а)ультрафиолетовой б)видимой в)инфракрасной). По какой формуле вычисляется частота излучения?

Уровни энергии атома водорода

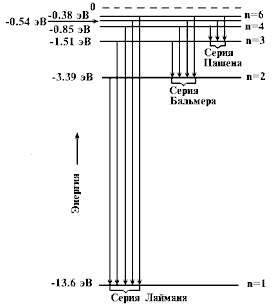
Электрон в атоме водорода переходит с 5-го на 3ий уровень. В какой области спектра будет находится излучение?

Переходы из состояний с n = 4, 5, 6, … в состояние с n = 3 образуют серию Пашена (инфракрасное излучение).

Частота излучения

v = E/h [Гц]

16.Изобразите на рисунке уровни энергии атома водорода и покажите переходы электрона, соответствующие серии Бальмера (см.Уровни энергии атома водорода).

Какие значения должны иметь n и k в сериальной формуле Бальмера, чтобы возникшее излучение имело максимальную частоту?

Переходы из состояний с n = 3, 4, 5, … в состояние с n = 2 образуют серию Бальмера (видимый свет)

Формула, описывающая серию Бальмера в спектре водорода

λ = 1/R(1/m² – 1/n²)

R=1,1⋅10¹⁷ м^-1 - постоянная Ридберга.

m - номер орбиты, на которую переходит электрон, n - номер орбиты, на которой находится электрон.

серия Бальмера – видимая серия спектра атомарного водорода. Энергия излучения данной серии выражается формулой:

E=h⋅c⋅R⋅(1/2²−1/n²),n=3,4,5,...

где R = 1,097∙10⁷ м^-1 – постоянная Ридберга, h = 6,63∙10^-34 Дж∙с – постоянная Планка, 

с = 3∙10⁸ – скорость света. Максимальная энергия будет при условии, что n будет очень большим (электрон в атоме переходит с уровня с очень большим номером на второй уровень). В этом случае 1/n² будет стремится к нулю (1/n² ≈ 0). Тогда максимальная энергия кванта

E_max=h⋅c⋅R/4.

18. Гипотеза Де Бройля

Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.

Итак, согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия Е и импульс р, а с другой — волновые характеристики — частота v и длина волны X. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов:

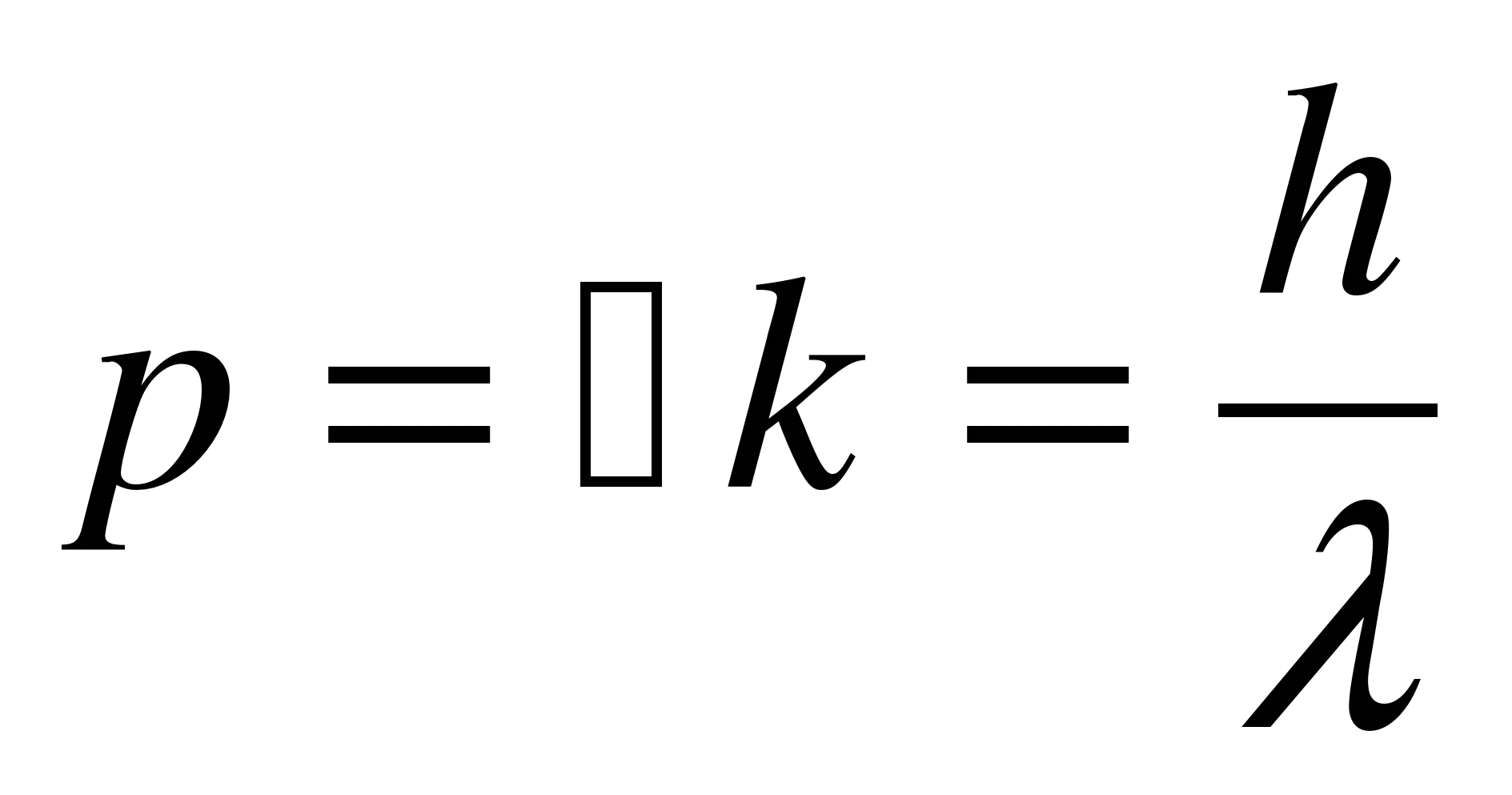
Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс, длина волны которого определяется по формуле де Бройля:

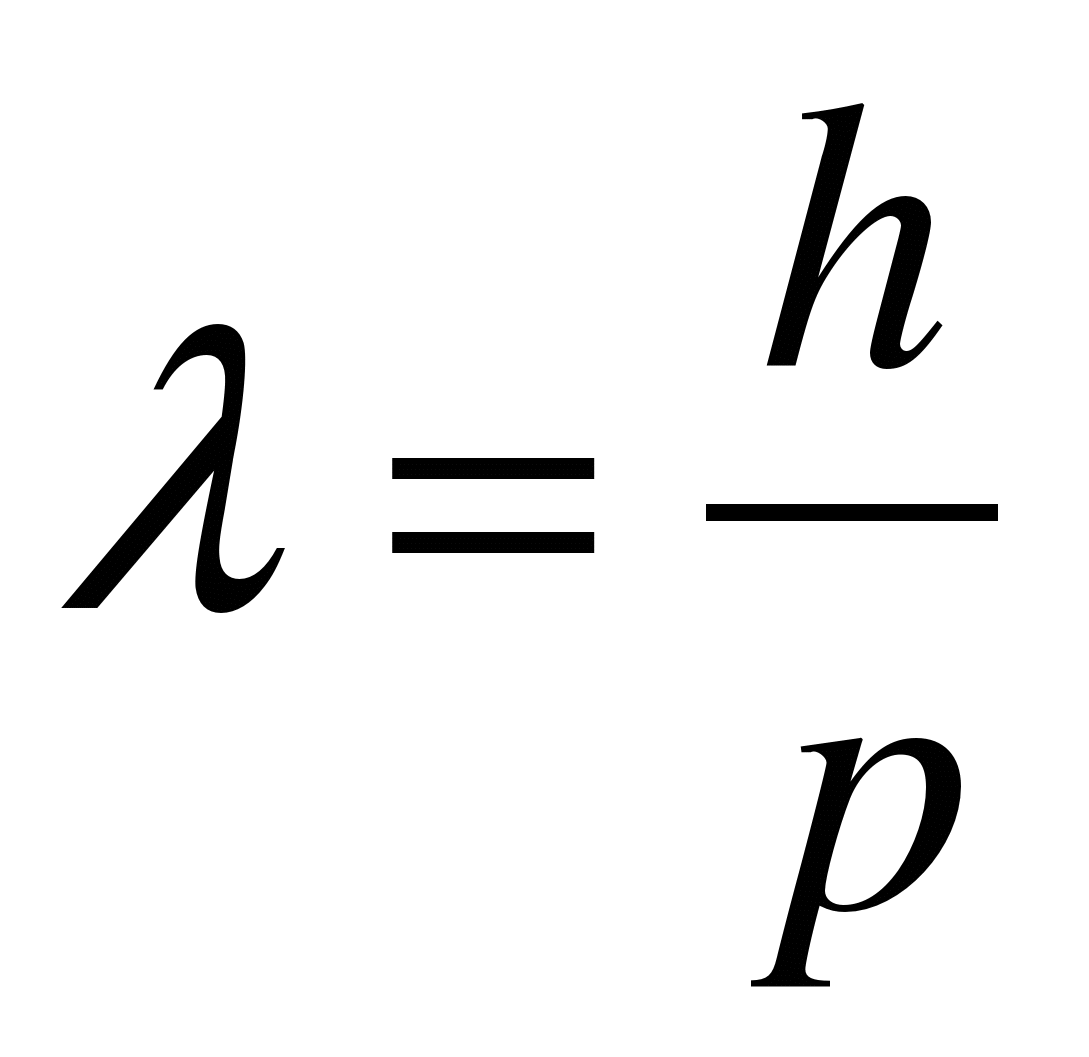
19. Стационарное уравнение Шредингера

Уравнение справедливо для любой частицы (со спином, равным 0), движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью v <C с.

Уравнение Шредингера имеет вид:

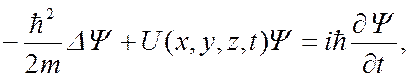
Где: m –масса частицы, i – мнимая единица,

– потенциальная функция частицы в силовом поле, в котором она движется,

– искомая волновая функция,

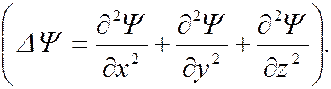∆ – оператор Лапласа

20. Принцип неопределенности Гейзенберга. Каким соотношением он выражается?

Объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой, и импульсом.

Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (x,y,z), и определенную соответствующую проекцию импульса (px,py,pz), причем неопределенности этих величин удовлетворяют условиям

т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.