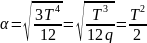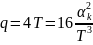2. Оптимальное по расходу энергии управление исполнительным двигателем постоянного тока

   1. Пусть под действием управления объект перемещается из начального в конечное состояние и описывается уравнениями состояния ; . Необходимо найти такое управляющее воздействие , чтобы энергетические затраты на перемещение объекта за время были бы минимальными.

Критерий оптимальности в этом случае имеет вид:

.

2. Для большей наглядности при рассмотрении данного вопроса будем опираться на данные, выполненной расчётно-графической работы

3. Задан исполнительный механизм – двигатель постоянного тока, питаемый от управляемого тиристорного преобразователя. Исполнительный механизм через редуктор перемещает рабочий орган из начального положения φ_о в конечное φ_к.

Рисунок 1 – Схема управления исполнительным механизмом

4. Для ОУ требуется найти управляющее воздействие, входящее для определенности в последнее уравнение:

(2.1)

Записываем функциональное уравнение (2.2) для объекта ОУ:

(2.2)

Коэффициент матрицы G принят равным единице, т.е. g₁(X) = 1. Подставляя уравнение ОУ (2.1) в (2.2), получим:

(2.3)

или

Требуется определить оптимальное управление по критерию расхода «сигнала управления». Тогда в соответствии со свойством 3 необходимо и достаточно выполнить условия:

(2.4)

В этом случае оптимальное управление будет иметь всего два интервала, причем на последнем интервале управление равно нулю, то есть объект (2.1) на втором интервале должен быть устойчив при отсутствии управления.

Определяя из (2.4) коэффициенты g₂(X), g₃(X), ..., g_n(X), подставляя их в уравнение (2.2) и интегрируя его, получим искомую функцию переключения и оптимальное управление.

5. Для примера выполним синтез оптимальной по энергосбережению («расходу сигнала» управления) привода с двигателем постоянного тока, уравнения которого имеют вид (2.5):

Будем считать уравнения (2.5) уравнениями возмущенного движения в соответствии с концепцией Ляпунова о возмущенном – невозмущенном движении.

Выразим из первого уравнения системы (2.5), - из второго, - из третьего и подставим их в четвертое уравнение системы (2.5). После группировки всех производных слева от знака равенства, обозначая их за производную от функции переключения регулятора положения , можно получить:

(2.6)

По функциональному уравнению (2.6) определяем, что для регулятора положение вала:

Интегрируя последнее уравнение и вводя задание по выходной координате (угловому положению вала исполнительного механизма), получим закон управления для регулятора положения вала привода.

6. Для примера приведено сравнение потерь энергии и производительности при реализации треугольного и прямоугольного управления САУ ИМ (таблица 1):

Таблица 1 – Таблица соответствия треугольной и прямоугольной диаграмм оптимальности

Тип схемы управления	Параметр
	Энергосбережение	Производительность	Быстродействие
	q		T
Δ
□
Расчёт соотношений
Краткий вывод	При использовании прямоугольной схемы управления потери выше на 33 %	При использовании треугольной схемы управления производительность выше на 15 %	При использовании треугольной схемы быстродействие выше на 11 %