4. Мнк для множественной регрессии

Метод наименьших квадратов (МНК) – один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Параметры модели выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений от модельных была минимальной

В общем виде линейную модель множественной регрессии можно записать следующим образом:

где   – значение i-ой результативной переменной,

x_1i…x_mi – значения факторных переменных;

β₀…β_m – неизвестные коэффициенты модели множественной регрессии;

ε_i – случайные ошибки модели множественной регрессии.

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов.

Суть метода наименьших квадратов состоит в том, чтобы найти такой вектор β оценок неизвестных коэффициентов модели, при которых сумма квадратов отклонений (остатков) наблюдаемых значений зависимой переменной у от расчётных значений ỹ (рассчитанных на основании построенной модели регрессии) была бы минимальной.

Матричная форма функционала F метода наименьших квадратов:

Следовательно,

Предпосылки МНК:

1. Случайный характер остатков

2. Нулевая средняя величина остатков, не зависящая от

3. Гомоскедастичность – дисперсия каждого отклонения одинакова для всех значений x

Пример гетероскедастичноти:

4. Отсутствие автокорреляции остатков. Значения распределены независимо друг от друга

5. Остатки подчиняются нормальному распределению

Коэффициенты интеркорреляции позволяют исключать из модели дублирующие факторы. 2 переменных коллинеарны, если . Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем 2 фактора связаны между собой линейной зависимостью. Чем сильнее коллинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью МНК.

Существуют другие линеаризуемые функции для построения уравнения множественной регрессии:

1. Экспонента:

2. Гипербола: , используется при обратных связях признаков

5. Теорема Гаусса-Маркова для множественной регрессии. Определение ковариационно – дисперсионной матрицы вектора коэффициентов регрессии.

Уравнение множественной регрессии:

Теорема Гаусса-Маркова:

Предположим, что:

1. 

2. X – детерминированная n x k матрица, имеющая максимальный ранг k

3. 

Тогда оценка МНК является наиболее эффективной (в смысле наименьшей дисперсии) оценкой в классе линейных (по y) несмещенных оценок.

По аналогии с парной регрессией построим оценку для вектора так, чтобы вектор оценок зависимой переменной минимально (в смысле квадрата нормы разности) отличался от вектора Y заданных значений:

Решением условия (14.5), если ранг матрицы равен , является оценка

Нетрудно проверить, что эта оценка несмещенная. Ковариационная (дисперсионная) матрица оценки равна

𝐷[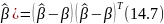

Доказана справедливость теоремы Гаусса - Маркова.

В условиях справедливости требований МНК оценка (14.6) является наилучшей (в смысле минимума дисперсии) оценкой в классе линейных несмещенных оценок.