20. Эконометрические модели с эволюционными изменениями коэффициентов

Модель с эволюционными изменениями коэффициентов в общем случае имеет следующий вид:

 

 

где ai(t), i=0,..., n – оценки коэффициентов модели, меняющиеся во времени под влиянием каких-либо факторов, условий.

Иными словами, предполагается, что значения оценок коэффициента ai, рассматриваемые в различные моменты времени, например, t и t+1, могут различаться между собой, т. е. ai(t)¹ai(t+1).

Заметим, что в общем случае выражение (9.37) можно интерпретировать как модель (п+1)×Т коэффициентами, поскольку в каждый момент t=1,2,..., Т значение ai(t) представляет собой как бы оценку “самостоятельного” коэффициента. Очевидно, что тогда определить весь набор значений ai(t), i=0,..., n, t=1,2,..., Т на основании Т независимых уравнений типа (9.37) не представляется возможным.

21. Точечные и интервальные прогнозы

Одной из прикладных целей эконометрического моделирования является построение прогнозных значений результативного показате­ля, при определенных значениях фактора. При этом, следует разли­чать предсказанное и прогнозное значения результативного показате­ля. Если в построенную модель парной регрессии подставляется значение фактора (х), входящее в интервал исходных данных [ ], то полученное значение результативного показателя называется предсказанием (у).

Если в построенную модель парной регрессии подставляется значение фактора (х), выходящее за рамки интервала исходных дан­ных [ ], то полученное значение результативного показателя называется прогнозным ( ). Однако следует помнить, что чем даль­ше расположено прогнозное значение фактора от границ интервала исходных данных, тем менее точным будет прогноз.

Следует различать точечный и интервальный прогноз.

Путем подстановки в уравнение регрессии соответствующего значения фактора , получают прогнозное значение результативного показателя - точечный прогноз. Однако точечный прогноз не является точным, так как на ре­зультативный показатель оказывают влияние случайные факторы в настоящем и будут влиять и в дальнейшем, причем сила и направле­ние их воздействия могут меняться. Поэтому целесообразно прогноз­ное значение результативного показателя представлять в виде дове­рительного интервала его возможных значений.

Для определения границ доверительного интервала необходимо точечное прогнозное значение результативного показателя скоррек­тировать на величину предельной ошибки . - стандартная ошибка прогноза, - табличное значение t-критерия Стьюдента. , где , n - количество наблюдений, m – количество объясняющих факторов.

После нахождения величины предельной ошибки 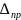корректируем точечное прогнозное значение результативного показателя на эту величину и определяем границы доверительного интервала.

– нижняя граница доверительного интервала

– верхняя граница доверительного интервала