изготовление, монтаж и испытание СЭУ / Лаба / Документ Microsoft Word (2)

Цель

Приобретение практических навыков проведения испытаний и обработки результатов с применением методов математической статистики.

Общие сведения

Испытания судового оборудования и судна в целом связаны с большим объемом измерений и использованием для этого различных приборов и измерительных систем.

При измерении практически любой величины получают не истинное значение, а лишь приближенное. Это связано с наличием систематических и случайных ошибок (погрешностей). Систематические погрешности могут быть учтены, так как связаны с вполне определенными причинами и изменяются по определенным законам. Случайные ошибки исключить невозможно, но математическая теория случайных величин позволяет уменьшить их влияние на окончательный результат измерений.

Чтобы оценить ошибку, необходима серия измерений. В основе теории погрешностей лежат два положения:

• при большом числе равноточных измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто;

• большие по абсолютной величине погрешности встречаются реже, чем малые т.е. вероятность появления погрешности уменьшается с ростом ее числового значения.

Допустим, что произведены п прямых измерений некоторой физической величины и получены результаты отдельных измерений х₁, Х₂, ..., х„.

Тогда случайная погрешность i - ого измерения

, (1)

где хо - истинное значение измеряемой физической величины.

Зависимость частоты появления случайных погрешностей от их величины описываются рядом функций.

Для большинства случаев наиболее приемлемым является нормальное распределение Гаусса (рис. 1)

где у — частота появления некоторою отклонения х относительно точного (истинного)значения;

- частота появления нулевого отклонения;

- так называемый модуль точности.

Рисунок 1 - Кривая плотности нормального распределения

Функция (2) описывает совокупность, содержащую бесконечное множество изменений. Нормальное распределение характеризуется рядом показателей, в том средним квадратическим отклонением а (или дисперсией ):

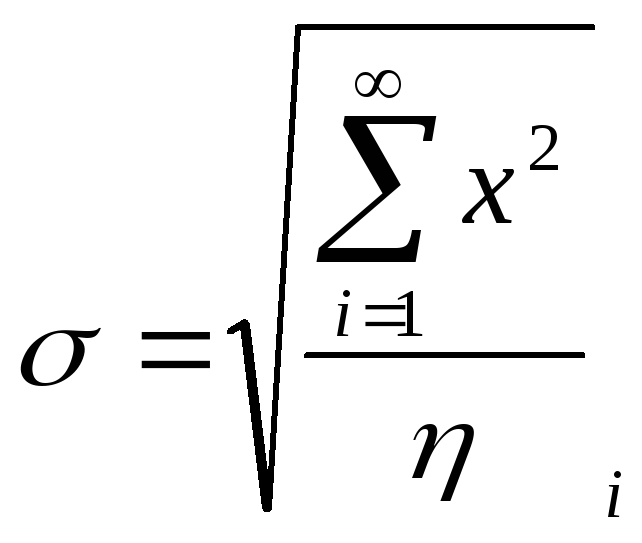
Ряд преобразований позволяет получить следующее соотношение:

В практических расчетах мы всегда имеем ограниченное число измерений (). Причем обычно истинное значение измеряемой величины неизвестно, поэтому в качестве наилучшей оценки точного или истинного значения в случае нормального распределения используется среднее арифметическое значение:

В этом случае точный результат для нахождения среднего квадратичного отклонения дает формула:

При. А при ограниченном числе измерений среднее арифметическое значение х_с будет сильно отличаться от истинного значения х_о т.е.

(7)

Вполне очевидно, что чем больше задаваемый доверительный интервал, чем с большей надежностью а в этот интервал попадает истинное значение. Например, при доверительном интервале может составлять 95% или в долях от единицы а = 0,9.

Переход от рассмотрения выборок с бесконечно большим числом измерений к меньшим выборкам приводит к необходимости введения ряда поправок. Опуская ряд теоретических выкладок, далее приводим расчетные зависимости. Среднее квадрати чес кое отклонение среднего арифметического х_с от истинного значения .

Для оценки границ доверительного интервала при малых значениях п должен > чнтываться коэффициент Стьюдента t_p,

Значение коэффициента Стьюдента t_p для разных значений надежности а приведены в таблице 1.

Таблица 1

Значение коэффициента Стьюдента

	0,9	0,95	0,98	0,99
2	6,31	12,71	31,82	63,66
3	2,92	4,30	6,96	9,92
4	2,35	3,18	4,54	5,84
5	2,13	2,78	3,75	4,60
6	2,02	2,57	3,36	4,03
7	1,94	2,45	3,14	3,71
8	1,90	2,36	3,00	3,50
9	1,86	2,31	2,90	3,36
10	1,83	2,26	2,82	3,25
15	1,76	2,14	2,62	2,95

Схема лабораторного стенда

1. воздуховод;

2. вентилятор;

3. поворотная заслонка;

4. расходомерная диафрагма;

5. дифманометр;

6. микроманометр;

7. воздушная головка (Dy25) судовой системы.

Практическая часть

Показания приборов, снятые во время испытания воздушной головки на лабораторном стенде, сведены в таблицу 2.

Таблица 2 Результаты измерений

№	, Па	Р, Па
		1	2	3	4	5	6
1	510	973	957	957	941	965	957
2	814	1491	1491	1483	1506	1506	1491
3	981	1765	1750	1773	1812	1812	1750
4	1275	2236	2220	2228	2252	2252	2220

Обработка результатов

1 Расчет коэффициента местного сопротивления воздушной головки.

Объемный расход воздуха определяется по полученной опытным путем аппроксимирующей формуле для используемого расхода:

, м³/с

где Ар - давление по дифманометру, Па.

Скорость потока в месте расположения датчиков статического давления микроманометра 6 определяется из соотношения:

F - площадь сечения трубы внутренним диаметром 48 мм на данном участке

(F = 0,0018 м²).

Коэффициент местного сопротивления воздушной головки в режиме всасывания : определяется по формуле:

где р - разрежение в сечении после воздушной головки по микроманометру. Па; р = 1,2 кг/м³ плотность воздуха (при температуре 20 °С). Результаты расчетов приведены в таблице 3.

Таблица 3 Расчет коэффициента местного сопротивления

№	V, м3/с	W, м/с	С
			1	2	3	4	5	6
1	0,0044	2,43	272	268	268	263	270	268
2	0,0055	3,07	418	418	415	422	422	418
3	0,0061	3,37	495	490	497	508	508	490
4	0,0069	3,85	627	623	625	632	632	623

2 Определение доверительных интервалов и определение погрешностей.

По таблице 2 для первой строки проводим расчеты.

Среднее арифметическое значение давление:

Среднее квадратическое отклонение:

=

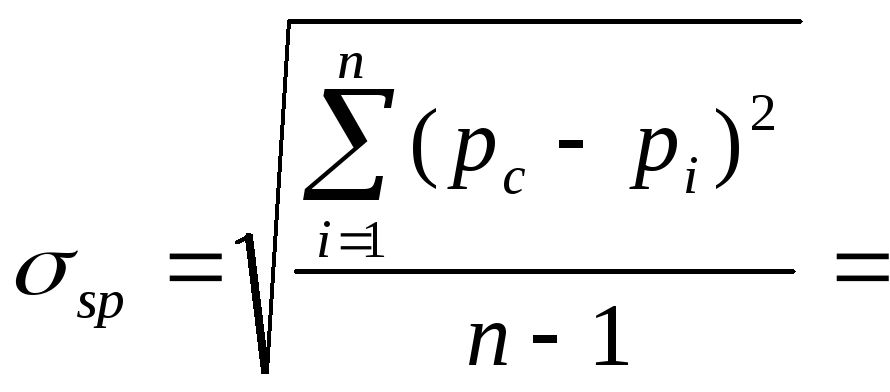
=10,43 Па

Среднее квадратическое отклонение среднего арифметического значения:

Среднее квадратическое отклонение величины

мм вод. ст. = 4,905 Па

Где t = 1 мм – цена деления.

Среднее арифметическое значение коэффициента местного сопротивления воздушной головки:

Погрешность косвенного измерения

Значение доверительного интервала:

Где -коэффициент Стьюдента (n=6,a=0.95).

Вычисления для остальных строк проводим аналогично. Результаты приведены в таблице 4.

Таблица 4

№ строки
1	958	10,43	4,25	268,47	3,9	10,02
2	1495	9,61	3,92	419,21	3,69	9,49
3	1777	28,83	11,77	498,62	8,46	21,75
4	2235	14,4	5,87	627,29	4,70	12,1

По результатам строим график зависимости представленный на рисунке 3.

V	0,006964	0,006108	0,005564	0,004404

Вывод:

В результате экспериментального исследования была определена зависимость коэффициента местного сопротивления дроссельной шайбы ζ от расхода воздуха V и рассчитан доверительный интервал Δх для степени надежности а =0,95.