1.2.2 Расчёт погрешности силового элемента (контактной пружины)
На величину усилия, при которой возникают деформации пружины, влияет конструктивно-технологический фактор. Причём он имеет случайный характер.
Расчёт усилия винтовых цилиндрических пружин производится по формуле:
F=
,
где G – модуль сдвига, Н/мм2; d – диаметр проволоки, мм; f2 – полная деформация пружины, мм; D0 – средний диаметр пружины, мм; ѡ – число витков пружины.
В формуле каждая составляющая имеет погрешность, так же влияет сплав, покрытие, наклёп.
Продифференцировав это выражение по каждой составляющей и перейдя к конечным приращениям, а затем разделив на F, получим значения частных погрешностей усилия F пружины, вызванные отклонениями соответственно диаметров проволоки и пружины, числа рабочих витков, длины пружины и модуля сдвига материала.
По вероятностному методу суммарная относительная погрешность контактного усилия вычисляется по формуле:
,
где t – коэффициент, выбираемый в соответствии с процентом риска;
λ – коэффициент, учитывающий закон распределения погрешности;
ΔFd / F – погрешность, зависящая от отклонений диаметра проволоки;
ΔFD / F – погрешность, зависящая от отклонений диаметра пружины;
ΔFW / F – погрешность, зависящая от отклонений числа витков пружины;
ΔFl / F – погрешность, зависящая от отклонений на высоту пружины;
ΔFG / F – погрешность, зависящая от отклонений модуля сдвига.
Продифференцируем по каждой переменной:
.
Погрешность, зависящая от отклонений диаметра проволоки:
%,
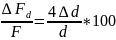где Δd – поле допуска по диаметру провода; по прил. 9
Δd = 0,02 мм.
Погрешность, зависящая от отклонений диаметра пружины:
,
где ΔD0 – поле допуска по диаметру пружины; по прил. 10
ΔD0 = 0,36 мм
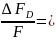(3*0,36/7)*100=15%.
Погрешность усилия, зависящая от отклонений числа витков пружины:
где ΔW – поле допуска на число витков пружины; по прил. 11
ΔW = 1.
.
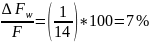Погрешность усилия, зависящая от отклонений длины пружины:
%,
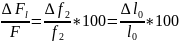где Δl – поле допуска на длину пружины, мм; по прил. 12 при
f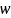
1=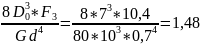
c1=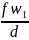
=1,48/0,7=2,11
∆l0=∆l1* =2*0,13*14=3,64
∆l1-предельные отклонения пружины в свободном состоянии (мм).
∆l1=±0,13
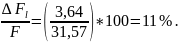
Определяем погрешность контактного усилия, зависящую от отклонений модуля сдвига материала проволоки:
,
где ΔG – погрешность модуля сдвига, МПа; ΔG = 1000.
.
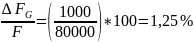Задаём
процент риска Р = 0,27 %, по прил. 13 поправочный
коэффициент f
= 3. В расчётах учитывается, что погрешности
подчиняются закону нормального
распределения, поэтому
=
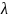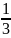
Тогда суммарная относительная погрешность контактного усилия:
.
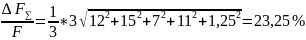1.3 Определение номинальных размеров конструкции
1.3.1 Определяем номинальные размеры
Определение номинальных размеров измерительных механизмов, известны номинальные значения пружины L1,L2,L0, диаметр проволоки, конструктивная компоновка.
Некоторые размеры задаются конструктивно.
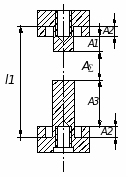
1
2
Рисунок 4 - Эскиз для расчета размеров А3: 1- фланец, 2- упор
Рисунок 5 - Размерная схема для определения размера А3
Уравнение размерной цепи имеет вид:
A∑=l1-A1-A2-A3-A2
таким образом, получается:
A3=l1-A1-2A2- A∑=24-3-2*2*1-8=9мм
Определили конструктивные элементы.
Следующая схема нужна для определения допусков обеспечивающая A∑; необходимо чтобы в уравнение схемы не попала пружина l1.
Задаём размеры:
A∑=8мм
d=1мм
A2=2d=2мм
A1=3мм
L1=24мм
A3=9мм
А4=А1+А2+3=8мм
А5=4мм
А6=х
А7=А5+2А5=12мм
А8=А3+А2+3=14мм
Рисунок – 6 Крышка
1
2
Рисунок - 7: 1- фланец, 2- упор
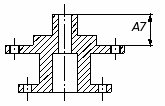
Рисунок – 8 Основание
Рисунок – 9 Крышка
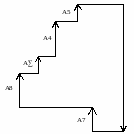
А6
Рисунок 10 –Размерная схема для определения размера А6
Уравнение размерной цепи имеет вид:
А6=А7+А8+ A∑+А4+А5=12+14+8+8+4=46мм.