Контрольная работа №6 теория функций комплексного переменного Вариант №1
Найти все значения корня комплексного числа.
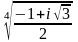
Представить комплексное числа в алгебраической форме.
Arctg (2-i).
Изобразить область, заданную неравенствами.
|z+i|≤2, |z-i|>2.
Проверить, что u является действительной частью аналитической функции. Восстановить аналитическую в окрестности точки z0 функцию f(z) по известной действительной части u(x,y) и значению f(z0).
u=x3-3xy2-x, f(0)=0.
Вычислить интеграл от функции комплексного переменного по заданной кривой.
;
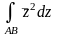AB – отрезок прямой, zA=0, zB=1+i.
Найти все разложения функции f(z) в ряд Лорана по степеням ( z-z0).
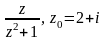
Найти все разложения функции f(z) в ряд Лорана в окрестности точки z0.
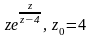
Для данной функции f(z) найти изолированные особые точки и определить их тип.
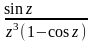
Найти вычеты функции f(z).
f(z)
=
.
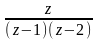Вычислить интеграл.
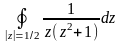
Вычислить интеграл.
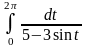
Вариант №2
Найти все значения корня комплексного числа.
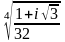
Представить комплексное числа в алгебраической форме.
Arch (3i).
Изобразить область, заданную неравенствами.
|z+1|≥1, |z+i|<1.
Проверить, что u является действительной частью аналитической функции. Восстановить аналитическую в окрестности точки z0 функцию f(z) по известной действительной части u(x,y) и значению f(z0).
u=-2xy-2y, f(0)=i.
Вычислить интеграл от функции комплексного переменного по заданной кривой.
;
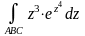ABC – ломаная, zA=i, zB=1, zC=0.
Найти все разложения функции f(z) в ряд Лорана по степеням z.
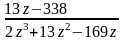
Найти все разложения функции f(z) в ряд Лорана в окрестности точки z0.
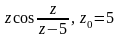
Для данной функции f(z) найти изолированные особые точки и определить их тип.
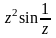
Найти вычеты функции f(z).
f(z)
=
.
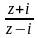Вычислить интеграл.
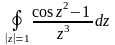
Вычислить интеграл.
Вариант №3
Найти все значения корня комплексного числа.
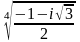
Представить комплексное числа в алгебраической форме.
Arcsin 4.
Изобразить область, заданную неравенствами.
|z-1|<1, arg z≤π/4, arg (z-1)>π/4.
Проверить, что u является действительной частью аналитической функции. Восстановить аналитическую в окрестности точки z0 функцию f(z) по известной действительной части u(x,y) и значению f(z0).
u=x/(x2+y2) x, f(1)=2.
Вычислить интеграл от функции комплексного переменного по заданной кривой.
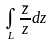;L
– граница области: {1<|z|<2,
Re z>0}.
Найти все разложения функции f(z) в ряд Лорана по степеням z.
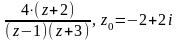
Найти все разложения функции f(z) в ряд Лорана в окрестности точки z0.
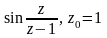
Для данной функции f(z) найти изолированные особые точки и определить их тип.
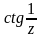
Найти вычеты функции f(z).
f(z)
=
.
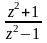Вычислить интеграл.
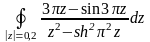
Вычислить интеграл.
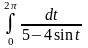
Вариант №4
Найти все значения корня комплексного числа.
.
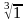Представить комплексное числа в алгебраической форме.
2. (-i)5i .
Изобразить область, заданную неравенствами.
|Re z|≤1, |Im z|<2.
Проверить, что v является мнимой частью аналитической функции. Восстановить аналитическую в окрестности точки z0 функцию f(z) по известной мнимой v(x,y) части и значению f(z0).
v=e-ysin x, f(0)=1.
Вычислить интеграл от функции комплексного переменного по заданной кривой.
; AB:{y=x2; zA=0, zB=1+i}.
Найти все разложения функции f(z) в ряд Лорана по степеням z.
.
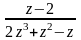Найти все разложения функции f(z) в ряд Лорана в окрестности точки z0.
.
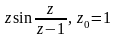Для данной функции f(z) найти изолированные особые точки и определить их тип.
.
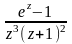Найти вычеты функции f(z).
f(z)
=
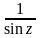относительно
полюса z
= π.
Вычислить интеграл.
.
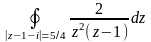Вычислить интеграл.
