Декурсивный и антисипативный способы начисления процентов

Декурсивный способ начисления процентов – наращение первоначальной суммы по процентной ставке. Проценты (правильнее - процентные деньги) выплачиваются в конце каждого интервала начисления.

Декурсивная процентная ставка (i), называемая ссудным процентом, – это выраженное в процентах отношение суммы начисленного за определенный интервал дохода I (процентных денег) к сумме, имеющейся на начало данного интервала - P. Наращение (рост) первоначальной суммы долга – увеличение суммы долга за счет присоединения начисленных процентов.

Суть его сводится к тому, что проценты начисляются в начале расчетного периода, при этом за базу (100%) принимается сумма погашения долга. В этом случае применяется не процентная, а учетная ставка (d). Такой метод начисления процентов носит название антисипативный (предварительный или авансовый).

Например, при использовании антисипативного метода выдан кредит сроком на один год в размере 800 тыс.руб. под 11% годовых. В этом случае заёмщик получит только 800-800*0,11=712 тыс.руб., а фактическая, т.е. реальная ставка будет равна

Сумма долга, подлежащая возврату(наращенная сумма), при антисипативном методе начисления процентов, производится по формуле:

где S – сумма долга (наращённая сумма);

P - капитал, предоставляемый в кредит;

n - продолжительность кредита в годах;

d - учетная ставка, выраженная десятичной дробью;

– множитель наращения.

В случае если учетная ставка выражена в процентах, множитель наращения имеет вид:

Пример 1.8.

Клиент обратился в банк за кредитом в сумме 800,0 тыс. руб. на срок 270 дней. Банк согласен предоставить кредит на следующих условиях: заёмщик выдаст вексель, обеспечивающий банку доходность от этой операции в размере 12% годовых. Расчет производится с использованием учетной ставки.

Надо определить сумму долга, которая должна будет проставлена в векселе.

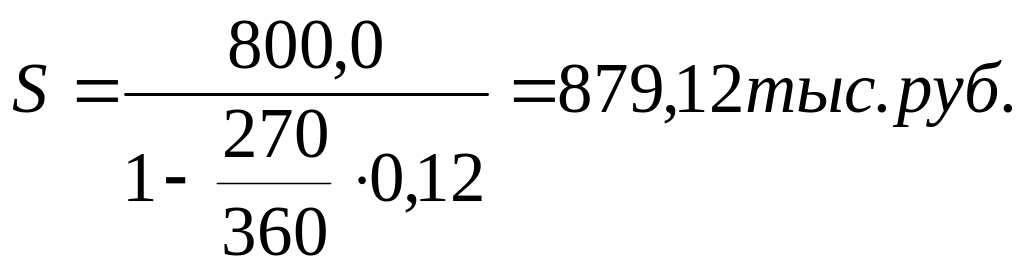
Если бы по приведенным данным начисление процентов производилось по простой процентной ставке, то наращенная сумма оказалась бы значительно меньше:

Таким образом, мы убедились, что простая учетная ставка дает более быстрый рост наращенной суммы, чем аналогичная по величине ставка простых процентов.

При равенстве простой процентной ставки (i) и простой учетной ставки (d) различие в величине множителей наращения определяется сроком ссуды, что показано в табл. 1.1.

Таблица 1.1

Множители наращения по простой ставке процентов и учетной ставке

(i =d =12.0%)

Вид ставки	Срок ссуды в годах
	1/12	1/4	1/2	1,0	2,0	5,0
i	1,01	1,03	1,06	1,12	1,24	1,60
d	1,01	1,0309	1,0638	1,136	1,3157	2,5

1.9. Дисконтирование. Математическое дисконтирование

Дисконтирование — это определение стоимости денежного потока путём приведения стоимости всех выплат к определённому моменту времени. Дисконтирование является базой для расчётов стоимости денег с учётом фактора времени.

В широком смысле дисконтирование определяется как средство нахождения любой стоимостной величины относящаяся к будущему на более ранний момент времени. Такой прием часто называют приведением стоимостного показателя к некоторому моменту времени.

Принимают два вида дисконтирования:

– математическое (ставка наращения);

– банковское (учетная ставка).

При математическом дисконтировании решается задача, обратная определению наращенной суммы. Сформулируем ее следующим образом: какую сумму следует выдать в долг на n лет, чтобы при начислении на нее процентов по ставке i получить наращенную сумму, равную S?

Для решения этой задачи используем формулу наращения по простой ставке процентов (1.4), тогда:

S= P+I= Р + P*n*i = P(1+n*i), (1.4)

(1.42)

где — дисконтный множитель, показывающий, во сколько раз первоначальная сумма ссуды меньше наращенной.

Пример 1.18.

Через один год владелец векселя, выданного коммерческим банком, должен получить по нему 220 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если доходность векселя должна составить 10% годовых?

Решение:

Находим современную (текущую)стоимость:

Пример 1.19.

Владелец векселя, номинальная стоимость которого 220 тыс. руб. и сроком обращения 1 год, предъявил его банку для учета за 90 дней до даты погашения. Банк учел его по ставке 12% годовых.

Определить дисконтированную величину (полученную владельцем векселя величину и величину дисконта).

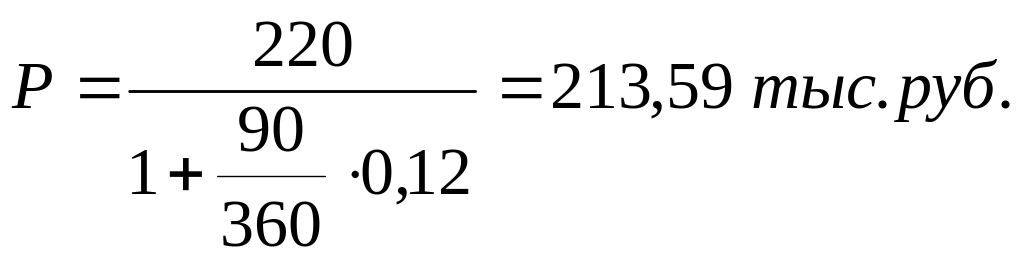— это сумма, полученная владельцем векселя в результате его учета.

Разность S-P=D’ является дисконтом.

В нашем случае дисконт равен:

D’=220-213,59=6,41 тыс.руб.

Действительно, если бы владелец векселя, получивший после его учета 213,59 тыс. руб., вновь поместил его в банк на 90 дней под 12,0% годовых, то по истечении указанного срока он бы получил 220 тыс. руб.

На практике в подобном случае банк обязательно установит для учета ставку более высокую, чем приведена в примере (12,0%), с целью получения большего дисконта, например 13,0%.