Задача №1 (электронный вид)

10

Задача

Напряженно состояние материала (сталь40, Ɠ_т=340МПа) в исследуемой точке тела характеризуется тензором . Исследовать напряженно состояние и определить направляющие косинусы нормали к главным площадкам в этой точке.

T_Ɠ ==

Решение

1. Определяем главные напряжения в рассматриваемой точке. Главные напряжения определяем, решая кубическое уравнение:

(инвариантная формула)

70+210+70=350

=3675

=(-3858750)

а=(-350)

b=3675

c=3858750

Перейдем от канонического вида кубического уравнения к приведенному виду.

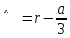
– приведенное уравнение.

Рассчитаем p и q:

=(-37158,33)

=1111574,07

Вернемся к приведенному уравнению.

Для определения количества корней подсчитаем дискриминант D.

Дискриминант меньше нуля, следовательно, существует 3 действительных корня.

=

𝜑 =

=

=

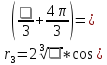
Проверка решения.

1. 

2. 

3. 

Выполненная проверка показала, что определение главных напряжений выполнено с достаточной точностью.

Тензор напряжений можно записать через главные напряжения.

=

2. Находим направляющие косинусы нормали к главным площадкам.

1. Для вычисления направляющих косинусов( , , ) к нормали - первой главной площадке, используем систему уравнений:

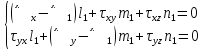
Разделим на и введем обозначения.

;

=

2. Для вычисления направляющих косинусов( , , 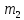) к нормали - второй главной площадке, используем систему уравнений:

Разделим на и введем обозначения.

;

=

Проверим ортогональность первой и второй нормали.

Получили результат близкий к нулю, что подтверждает правильность расчета направляющих косинусов первой и второй нормали.

3. Для вычисления направляющих косинусов( , , ) к нормали 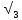- третьей главной площадке, используем систему уравнений:

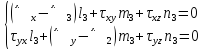
Разделим на и введем обозначения.

;

=

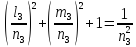
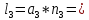
Проверим ортогональность первой и третьей нормали.

Получили результат близкий к нулю, что подтверждает правильность расчета направляющих косинусов первой и второй нормали.

Проверим ортогональность второй и третьей нормали.

Получили результат близкий к нулю, что подтверждает правильность расчета направляющих косинусов первой и второй нормали.

3. Изображаем положение нормали , , к трем главным площадкам. Положение каждой нормали наносится на чертеж по трем её проекциям на оси координат. Проекции единичных нормалей , , на оси координат составляют:

4. Вычисляем октоэдрические напряжения.

5. Находим максимальные касательные напряжения.

Наибольшим среди максимальных касательных напряжения является напряжение

6. Определяем нормальные напряжения на площадках действия максимальных касательных напряжений.

7. Проверяем прочность выбранного материала по критерию эластичности Мизеса.

Согласно критерию Мизеса: пластичное состояние материала наступает, когда интенсивность напряжения равна пределу текучести .

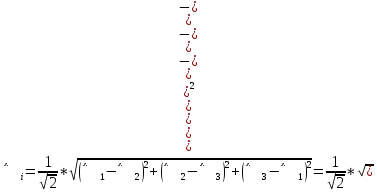
Предел текучести рассматриваемого материала составляет Сравнивая значения приходим к выводу, что согласно критерию Мизеса рассматриваемый материал не достигает состояния пластичности.