30. Квантовые теории теплоёмкости эйнштейна и дебая. Фононы

Классическая теория теплоёмкости имеет ограниченное применение, так как её теоретические выводы не всегда согласуются с экспериментом.

Классическая теория не даёт объяснения зависимости теплоёмкости газов от температуры. Из простых формул для расчета теплоёмкостей (C_p = (i + 2) R/2 и C_V = iR/2) следует, что молярные теплоёмкости газов определяются лишь числом степеней свободы и не зависят от температуры. Это справедливо только для одноатомных и многих двухатомных газов (Н₂, О₂, N₂) при комнатной температуре. У трехатомных газов теоретические и экспериментальные результаты сильно отличаются.

Рассмотрим температурную зависимость теплоемкости C_V для водорода, показанную на рис. 84. Из графика видно, что при повышении температуры проис­ходит как бы «включение» различных степеней свободы: при малой температуре включаются лишь поступательные степени свободы, а затем вращательные и колебательные. Это явление объясняет квантовая механика, согласно которой энергия может принимать не любое значение, а только дискретный ряд значений. Энергия может меняться только скачками. Упро­щённая схема уровней энергии (вращательных и колебательных) схематически представлена на рис. 85. При низких температурах энергия теп­лового движения меньше разности энергий соседних уровней (kT << ), и при столкновениях молекул вращательные и колебательные степени свободы не возбуждаются. Поведение двухатомного газа подобно одноатомному. Так как разность между соседними вращательными уровнями энергии значительно меньше, чем между колебательными (_ВРАЩ << _КОЛЕБ), то с ростом температуры возбуждаются вначале вращательные степени свободы, в результате чего теплоёмкость возрастает; при дальнейшем росте температуры возбуждаются и колебательные степени свободы и происходит дальнейший рост теплоёмкости.

Плавные переходы на температурном графикеC_V между дискретными уровнями (рис. 84) объясняются тем, что согласно распределению молекул по скоростям и энергиям лишь какая-то доля молекул от общего числа первоначально имеет энергию, достаточную для возбуждения вращательного и колебательного движений.

Согласно классической теории теплоёмкость металлов должна складываться из теплоёмкости кристаллической решетки, равной 3R (закон Дюлонга и Пти), и теплоёмкости электронного газа, равной 3R/2 (электрон как материальная точка имеет среднюю кинетическую энергию, равную 3kT/2). Таким образом, атомная теплоёмкость металлов должна быть близка к 4,5R. Однако опыт показывает, что она равна 3R. Это объясняет квантовая механика. Известно, что функции распределения Ферми-Дирака для Т = 0 и для Т > 0 различаются лишь в узкой области энергий порядка нескольких kT. Следовательно, в процессе нагревания металла участвует лишь незначительная доля от всех электронов проводимости. Поэтому отсутствует заметная разница между теплоёмкостями металлов и диэлектриков (3R), что не могло быть объяснено классической теорией.

Классическая теория теплоёмкости не объясняет температурную зависимость молярной теплоёмкости твёрдых тел, показанную на рис. 86, которая в области низких температур пропорциональна кубу температуры.

Простейшая квантовая теория была предложена Эйнштейном. В этой теории кристалл рассматривался как система N атомов, каждый из которых являлся квантовым гармоническим осциллятором. Колебания всех атомов происходят независимо друг от друга с одинаковой частотой . Средняя энергия , приходящаяся на одну степень свободы атома квантового гармонического осциллятора, равна

^.

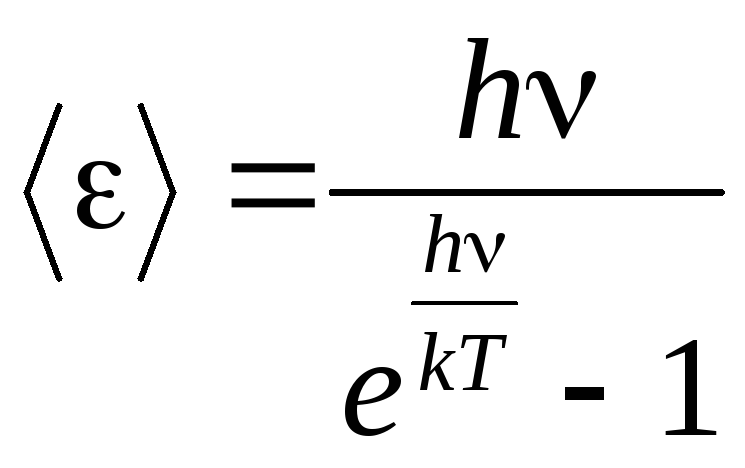Внутренняя энергия 1 моля твёрдого тела (с учетом 3 степеней свободы колебаний атома в узле решетки) выражается следующим образом:

^.

Для нахождения молярной теплоёмкости необходимо взять производную:

Дополнительно умножим

и разделим на k.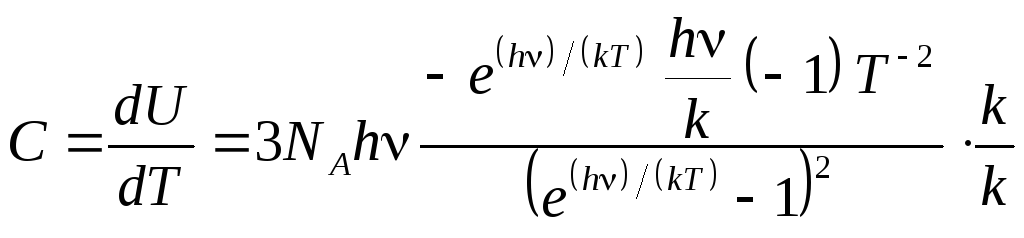

^.

Если ввести характеристическую температуру Эйнштейна

^{, то .}

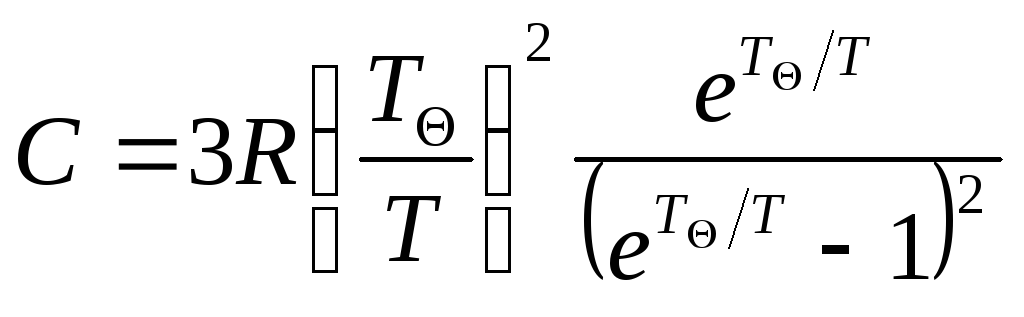Полученная формула Эйнштейна лишь качественно описывает зависимость теплоёмкости твёрдых тел от температуры: при высоких температурах (h << kT) теплоёмкость С  3R, а при Т  0 теплоёмкость С  0. Однако количественно поведение теплоемкости твёрдого тела вблизи абсолютного нуля описывается недостаточно точно.

Дебай развил упрощенную теорию Эйнштейна. В теории Дебая учтено, что колебания атомов в кристаллической решетке не являются независимыми. Между атомами твердого тела имеются настолько сильные взаимодействия, что все N частиц тела образуют связанную систему, обладающую 3N степенями свободы, причем колебания всех атомов могут происходить с разными частотами.

Рассматривая непрерывный спектр частот осцилляторов, Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам звукового (или ультразвукового) диапазона. Связь между частицами в кристаллической решетке приводит к тому, что в кристалле распространяются упругие волны.

Упругие волны в кристалле имеют квантовые свойства, проявляющиеся в том, что существует наименьшая порция – квант энергии волны с данной частотой. Это позволяет звуковой волне с частотой  сопоставить квазичастицу фонóн, который распространяется в кристалле со скоростью звука. Фонон обладает энергией E = h.

Квазичастицы, в частности фононы, сильно отличаются от обычных частиц (например, электронов, протонов, фотонов), так как они связаны с коллективным движением многих частиц системы. Квазичастицы не могут возникать в вакууме, они существуют только в кристалле. Импульс фонона обладает своеобразным свойством: при столкновении фононов в кристалле их импульс может дискретными порциями передаваться кристаллической решетке – он при этом не сохраняется. Поэтому в случае фононов говорят о квазиимпульсе.

Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняющегося статистике Бозе-Эйнштейна, так как фононы являются бозонами (их спин равен нулю). Фононы могут испускаться и поглощаться, но их число не сохраняется постоянным. Поэтому химический потенциал фононного газа равен нулю.

При вычислении внутренней энергии кристалла и его теплоёмкости вводится характеристическая температура Дебая:

^,

где – верхняя граница частот фононов, вносящих вклад в энергию тепловых колебаний кристалла (максимальная частота колебаний кристаллической решетки). При расчетах рассматривают два предельных случая:

а) при высоких температурах (T >> T_D) в результате вычислений получается закон Дюлонга и Пти: С = 3R;

б) при низких температурах (T << T_D) получается закон Дебая, из которого следует, что молярная теплоёмкость пропорциональна кубу температуры:

^.

ТРИЗ-задание 45. Премия и антипремия

Нобелевская премия присуждается за выдающиеся научные исследования и революционные изобретения. Эйнштейн и Дебай были лауреатами Нобелевской премии. С 1991 г. присуждается и Шнобелевская премия за достижения, которые невозможно воспроизвести или же нет смысла делать. Как одним словом охарактеризовать отличие одной премии от другой? (Кстати, этим словом называется один из изобретательских приёмов.)