19. Условия равновесия на границах различных сред

На поверхность одной жидкости нанесем каплю другой жидкости, не смешивающейся с первой и плотность которой меньше (чтобы капля не утонула). Например, поместим каплю масла (2-я среда) на воду (1-я среда). На границах различных сред будут действовать разные силы поверхностного натяжения (рис. 47).

Если , то жидкость 2 растекается по поверхности жидкости 1 в виде тонкого молекулярного слоя. В этом случае говорят ополной смачиваемости двух жидкостей.

Если , то жидкость 2 будет стягиваться в каплю до тех пор, пока не установится равновесие. Это векторное равенство в проекциях на осиX и Y распадается на два скалярных уравнения:

(возведём в квадрат)

Сложим два последних уравнения и упростим получившееся выражение при помощи тригонометрических формул:

,

, пусть ₁ + ₂ = ,

. (84)

Выражение (84) определяет условие равновесия плавающей капли. Углы ₁ и ₂ называются краевыми углами.

При  = 0 наступает полное смачивание, например, бензин или керосин на воде растекаются тонким слоем с радужной окраской, что объясняется интерференцией света.

Кроме сил поверхностного натяжения на каплю действуют сила гидростатического давления на поверхность S₁₂, сила тяжести, сила Архимеда. Однако на границе раздела нескольких веществ этими силами можно пренебречь, так как силы поверхностного натяжения значительно сильнее.

Аналогично ведет себя капля жидкости на поверхности твёрдого тела (рис. 48). Форма капли определяется силой тяжести и силой поверхностного натяжения. Условие равновесия капли в проекции на ось Х можно записать следующим образом:

^или .

Отсюда найдем краевой угол  при равновесии капли:

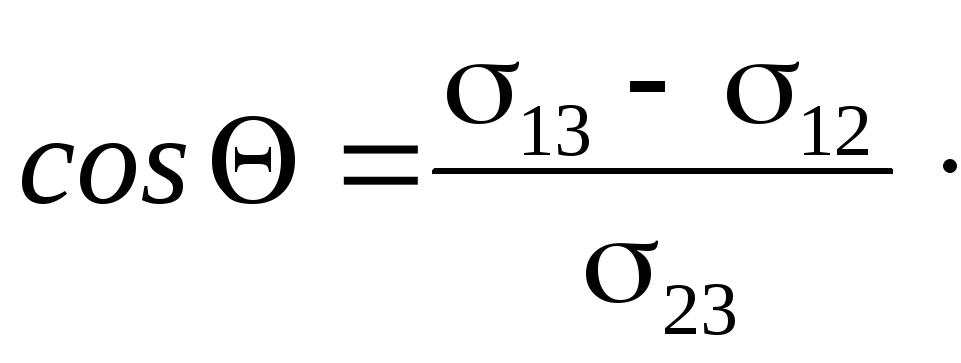(85)

Если (₁₃ – ₁₂)/₂₃ > 1 или ₁₃ > ₁₂ + ₂₃, то это означает, что сила F₁₃ больше суммы двух других сил, и жидкость тонким слоем растекается по твёрдому телу ( = 0). Это полное смачивание. Примеры: 1) вода на чистом стекле (проверка чистоты лабораторной посуды); 2) керосин на поверхности жести или стекла; 3) ртуть на химически чистой поверхности металла.

Если (₁₃ – ₁₂)/₂₃ < – 1 или ₁₂ > ₁₃ + ₂₃, то жидкость стягивается в каплю, несколько приплюснутую силой тяжести (рис. 49). Это полное несмачивание. Примеры: 1) вода на парафине; 2) ртуть на стекле.

В большинстве случаев имеет место частичное смачивание, когда краевой угол  – острый (рис. 50), или частичное несмачивание, когда краевой угол   тупой (рис. 51). При несмачивании силы притяжения между молекулами самой жидкости больше, чем между молекулами жидкости и твёрдого тела, а при смачивании – наоборот.

Если жидкость налита в широкий сосуд, то сила тяжести обеспечивает плоскую и горизонтальную поверхность. Однако благодаря несмачиванию или смачиванию у самых стенок сосуда образуется выпуклый или вогнутыймениск, т.е. искривление свободной поверхности жидкости около стенок (рис. 52).

При плавании тел из-за эффекта смачивания возникает дополнительная сила, которая либо увеличивает подъёмную силу, либо уменьшает её (рис. 53). Например, могут плавать фольга, иголка или лезвие бритвы.

ТРИЗ-задание 31. Поверхностное натяжение твёрдых тел

Наличие силы F₁₃ на рис. 48 говорит о том, что поверхностным натяжением обладают не только жидкости, но и твёрдые тела. Действительно, если на рис. 41 слово «жидкость» заменить на слова «твёрдое тело», то ничего не изменится ни в рисунке, ни в рассуждениях, поскольку и в жидкости, и в твёрдом теле молекулы расположены близко друг к другу. Поверхностное напряжение твёрдого тела в своё время стало причиной брака при производстве полупроводниковых пластин (толщиной 100 мкм и диаметром 40 мм и выше). В.В. Митрофановым было обнаружено следующее явление: кремниевая пластина, стороны которой были обработаны различно – одна сторона полированная, а другая шлифованная (грубо обработанная), изгибается, причем всегда полированная поверхность вогнутая, а шлифованная – выпуклая. Пластинки даже самопроизвольно ломались. Как этого избежать?

Описанный эффект – этоэффект Тваймана. Попробуйте сделать несколько изобретений, применив эффект Тваймана для выдвижения идей принципа действия различных измерительных приборов.

В.В. Митрофанов на основе этого и других эффектов сформулировал постулат о диссиметрии (какой?). Диссиметрия – причина любого явления или эффекта и ключ к решению всех загадок природы.

Найдите диссиметрию в явлениях молекулярной физики.