24. Опорные вектора и их конусы. Теоремы существования. Свойства

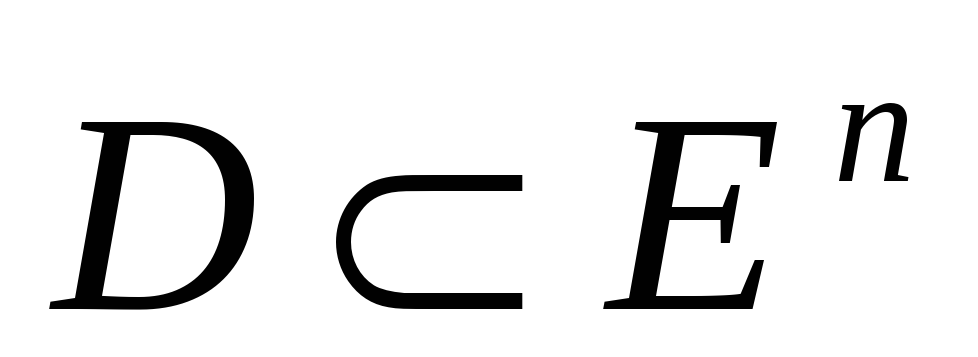Определение 1. Вектор называется опорным в точке ко множеству , если выполняется неравенство

При этом для гиперплоскость называется опорной в точке к множеству .

Легко увидеть, что опорные векторы определяются не единственным образом.

Обозначим через множество опорных векторов в точке к множеству . Иногда множество векторов опорных в к будем обозначать .

Очевидно, что нулевой вектор всегда включается во множество , причем если , то . Далее в этом разделе мы изучим условия существования ненулевых опорных векторов. Но прежде приведем следующее определение.

Определение 2. Вектор называется строго опорным в точке к множеству , если выполняется неравенство .

Очевидно, что строго опорный вектор является опорным. Обратное утверждение, вообще говоря, неверно.

Теорема 1. Пусть – выпуклое множество из и . Тогда существует вектор строго опорный в точке к множеству .

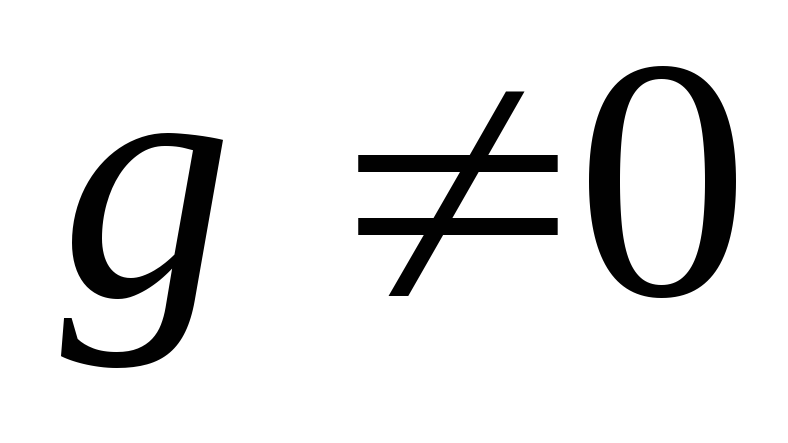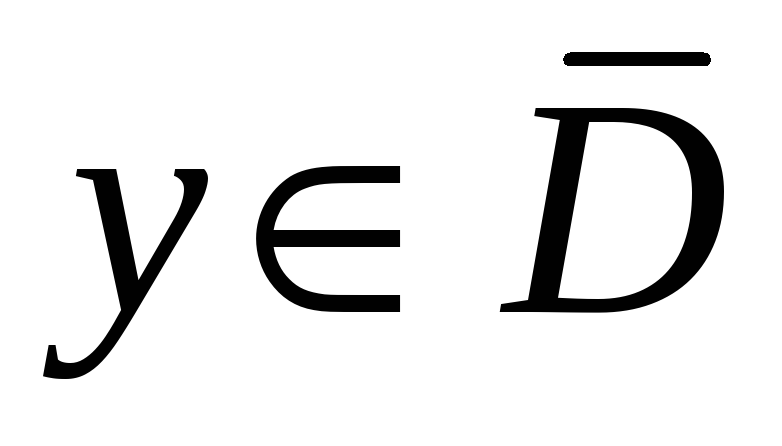Доказательство. Согласно теореме о существовании проекции . Обозначим для краткости и положим . Так как , вектор . Убедимся, что вектор – строго опорный к в точке . Из выпуклости множества следует выпуклость . Тогда неравенство справедливо для всех , а значит, и для всех 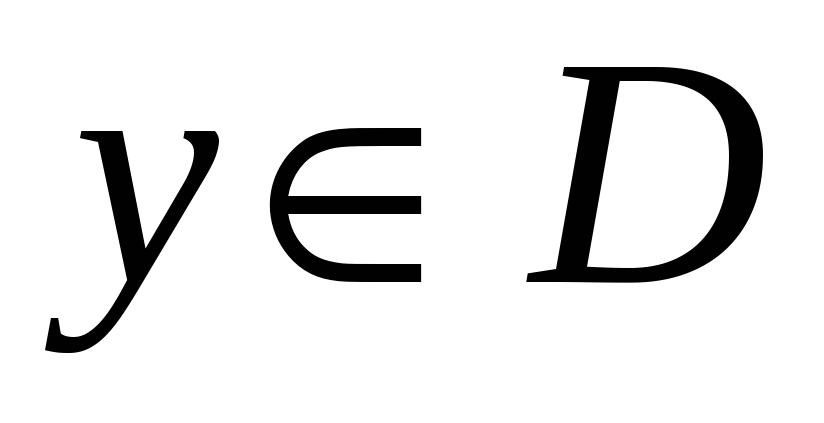. Преобразуем это неравенство следующим образом:

,

откуда . Что и требовалось.

Теорема 2. Пусть – выпуклое множество и . Тогда существует ненулевой опорный вектор в точке к множеству .

Доказательство. Если , то этот факт следует из теоремы 1. Пусть . Тогда из условия теоремы следует, что – граничная точка множества . Поэтому существует последовательность 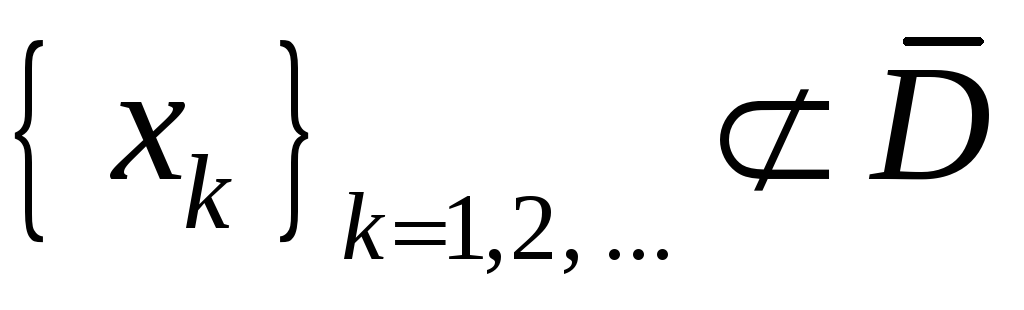такая, что . Согласно теореме 1 для любого существует ненулевой вектор строго опорный в точке 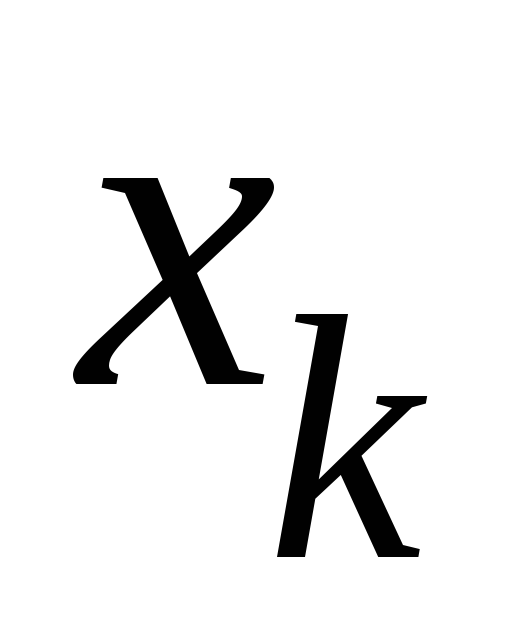к множеству . Следовательно, для всех имеем

. (1)

Не нарушая общности, можно считать, что для всех Поэтому последовательность имеет предельную точку. Также, без ограничения общности, будем считать, что эта последовательность сходится. Положим . Очевидно, что . Перейдем в (1) к пределу по . Получим . Таким образом, – опорный вектор в точке к множеству . Что и требовалось.

Замечание. Ненулевой опорный вектор в точке к множеству является строго опорным вектором в к множеству .

В прошлой лекции было введено множество векторов, опорных в точке ко множеству . Изучим свойства этих множеств.

Теорема 1. В любой точке множество является выпуклым замкнутым конусом.

Теорема 2. Пусть и – множества из ,

. Тогда .

Следующая теорема непосредственно вытекает из теорем 2 и 1.

Теорема 3. Пусть ,.

Тогда .

Задача построения конуса векторов, опорных для данного множества в данной точке, вообще говоря, является достаточно сложной. Не существует явных формул или конечных алгоритмов, решающих эту задачу в общем случае. Однако для некоторых классов множеств эта задача решается сравнительно просто. Рассмотрим далее несколько случаев таких множеств, которые нам потребуются в дальнейшем.

Теорема 4. Пусть , где функция определена, является выпуклой и непрерывно дифференцируемой на , точка такова, что . Тогда .

Получим теперь правило построения конуса опорных векторов для класса множеств, образованных системами выпуклых неравенств. Нам понадобится следующее условие.

Условие Слейтера. Пусть на определены функции , . Говорят, что система неравенств , удовлетворяет условию Слейтера относительно некоторого множества из , если существует точка такая, что для всех .

Если данная система неравенств удовлетворяет условию Слейтера относительно , то будем просто говорить, что она удовлетворяет условию Слейтера.

Для системы выпуклых неравенств выполнение условия Слейтера обеспечивает непустоту внутренности множества решений системы. То есть .

Теорема 5. Пусть – множество решений системы , удовлетворяющей условию Слейтера, все функции выпуклы и непрерывно дифференцируемы. Пусть точка такова, что . Тогда , где .

Теорема 6. Пусть , где – матрица размерности , вектор , точка такова, что . Тогда совпадает с конической оболочкой системы векторов , где – -тая строка матрицы .

Заметим, что эта теорема, вообще говоря, не является частным случаем теоремы 5, так как в ней не предполагается выполнение условия Слейтера.