моп / 35. Метод приведенного градиента

35. Метод приведенного градиента.

Метод приведенного градиента (МПГ) основан на сокращении размерности задачи с помощью представления всех переменных через множество независимых переменных. Впервые его предложил Вульф в (1963) для задач выпуклого программирования с линейными ограничениями. Позднее этот метод был обобщен на случай нелинейных ограничений. Итак, рассмотрим следующую задачу:

минимизировать                          (1)

при условиях

 ,                                       (2)

 ,                                           (3)

где A - матрица порядка mn ранга m; A_m - m-мерный вектор, а функция f(x) непрерывно дифференцируема. Сделаем следующее предположение о невырожденности матрицы :

Любые m столбцов A линейно независимы, и каждая крайняя точка допустимой области имеет ровно m положительных переменных и не более чем n-m нулевых компонент.

Пусть x - допустимая точка. По предположению о невырожденности матрица A может быть представлена в виде , где  - невырожденная матрица , а вектор , где  - базисный вектор, а  - небазисный вектор. Пусть , где  - градиент функции  по базисным переменным.

Вспомним, что направление  является возможным направлением спуска для функции  в точке , если  и  , если .

Определим возможное направление спуска  в данной задаче.

Представим вектор  в виде . Заметим, что равенство  автоматически выполняется, если для любого  положить Обозначим через

r^T = [r_B^T; r_N^T] = f ^T - _Bf ^TB^-1A = f ^T - _Bf ^TB^-1[B;H] =

= [0..0; _Nf ^T - _Bf ^TB^-1N] (4)

приведенный градиент.

Исследуем :

.                                  (5)

Необходимо выбрать  так, чтобы  и  если . Введем следующее правило. Для каждой небазисной компоненты  положим  , если  и возьмем , если . Это обеспечивает выполнение неравенства , если . Кроме того,  и строгое неравенство имеет место при .

Если , то  - возможное направление спуска. Кроме того,  тогда и только тогда, когда  - точка Куна-Таккера.

Алгоритм метода приведенного градиента

Рассмотрим алгоритм приведенного градиента (ПГ) для решения задачи (1)-(3). Предполагается, что любые  столбцов  линейно независимы.

Начальный этап. Выбрать точку , удовлетворяющую условиям . Положить =1 и перейти к основному этапу.

Основной этап. Первый шаг. Положить , где  и  получены по формулам (9) - (10) соответственно. Здесь  - множество индексов  наибольших компонент вектора ,

              (6)

                    (7)

                    (8)-(9)

 .                           (10)

Если , то остановиться,  - точка Куна-Таккера. В противном случае перейти ко второму шагу.

Второй шаг. Решить следующую задачу одномерной оптимизации:

минимизировать                       (11)

при условии                          ,

где                    (12)

Здесь  - -е компоненты векторов  соответственно. Положить _равным оптимальному и . Заменить k на k+1 и перейти к первому шагу.

Метод обобщенного приведенного градиента

Метод обобщенного приведенного градиента (ОПГ) является развитием метода ПГ и его можно использовать для решения задач НП при нелинейных функциях-ограничениях.

Итак, пусть задача НП задана в виде

минимизировать                        (13)

при условиях

 ,                              (14)

 .                                         (15)

В методе ОПГ также различают две группы переменных:

а) подмножество базисных переменных ;

б) подмножество небазисных, или независимых переменных . Примем для простоты обозначений . При этом зависимые (т.е. базисные) переменные неявным образом определяются через независимые (небазисные) переменные. Следовательно,  - функция  независимых переменных. Введем следующие обозначения:

(16)

Основная идея метода ОПГ состоит, как и в линейном случае, в том, чтобы сократить размерность задачи путем исключения зависимых (базисных) переменных и применить метод ПГ для определения направления спуска и в качестве критерия при установлении оптимальности.

Укажем способ вычисления обобщенного ПГ. Для этого рассмотрим задачу (13)-(15) и выразим обобщенный ПГ через компоненты градиента  и якобиан для ограничений-равенств (14)

 .                    (17)

Исключим из (17) матрицу . Для этого воспользуемся соотношением

 ,                   (18)

откуда

 .                         (19)

Подставляя (19) в (17), получим выражение для ОПГ, с учетом (16);

 ;                (20)

Нетрудно увидеть аналогию между выражением (20) и соотношением (4) для  ПГ   в   линейном   случае.  Действительно, если учесть, что  , то . Подставив их в (20), получим полное совпадение выражений (20) и (4).

Алгоритм метода ОПГ начинает работать с допустимой точки . Если же относительно условий задачи  не является допустимым, то необходимо ввести искусственные переменные, значения которых постепенно сводят к нулю путем введения в целевую функцию штрафного члена.

Если ОПГ ни на одном из этапов вычислительной процедуры не становится равным нулю, то заменяем текущий вектор  на   по общей формуле

 ,                              (21)

 - определяется путем решения задачи:

минимизировать при условиях             .

где  - направление оптимизационного поиска на k-й итерации.

Рассмотрим способ определения величин  для независимых переменных . Направления поиска  для них определяют следующим способом:

 , если ;                    (22)

 , если ;                   (23)

или       , где  - вектор ОПГ.

Если ограничения  линейны, то метод совпадает с методом Вульфа.

Пример 1.          Минимизировать при условии       .

Пусть  - независимая (небазисная) переменная, а  - зависимая. Найдем величины

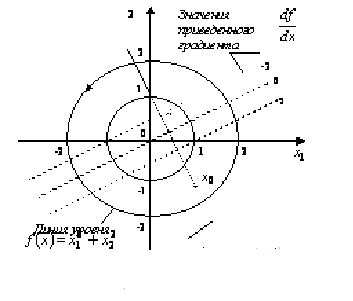
Рисунок 1

Согласно формуле (20) получим следующее выражение для ОПГ:

Итак, двигаясь из любой допустимой точки вдоль ограничения  до тех пор, пока  не станет равным нулю, выполняем минимизацию f (x) ( рис.1).