20. Понятие выпуклости (вогнутости) функции. Теорема о единственности экстремума строго выпуклой (вогнутой) функции. Док-во.

Определение 1. Функция , определенная на , называется выпуклой, если для любых и любого выполняется неравенство

. (1)

Если при и неравенство (1) выполняется как строгое, то функция называется строго выпуклой.

Определение 2. Функция , определенная на , называется вогнутой (строго вогнутой), если функция является выпуклой (строго выпуклой).

Очевидно, что любая строго выпуклая (строго вогнутая) функция является выпуклой (вогнутой) функцией, но не наоборот.

Теорема 3. Пусть – выпуклое множество

из , функция 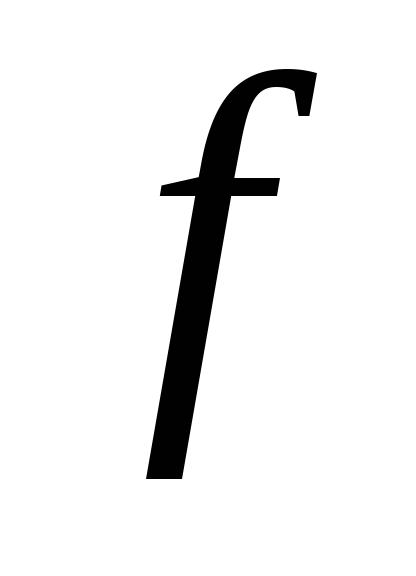– строго выпукла на . Тогда

множество содержит не более одной точки.

Доказательство. Пусть . Докажем, что оно состоит только из одной точки. Пусть это не так, то есть существуют два различных вектора . Тогда в силу выпуклости множества (см. предыдущую теорему) при любом , и в силу строгой выпуклости функции имеем

Полученное противоречие доказывает теорему.