моп / 15. Интерпретация (экономическая) множителей Лагранжа. Устойчивость

15. Интерпретация (экономическая) множителей Лагранжа. Устойчивость.

Представим классическую задачу условной оптимизации в виде ; , где - управляющие (внешние) переменные величины, представляющие в прикладных технических и экономических задачах переменные ресурсы – параметры задачи.

Для простоты изложения рассмотрим пример в с одним ограничением и параметром b:

. , где - переменная величина.

Пусть - точка условного экстремума. При изменении изменяются и , т.е. . Соответственно изменится и значение целевой функции: (b).

Вычислим полные производные в стационарной точке:

. (17)

(18)

Из grad L=0 в x* следует: , то есть

. (19)

Подставим (18), (19) в (17) и получаем:

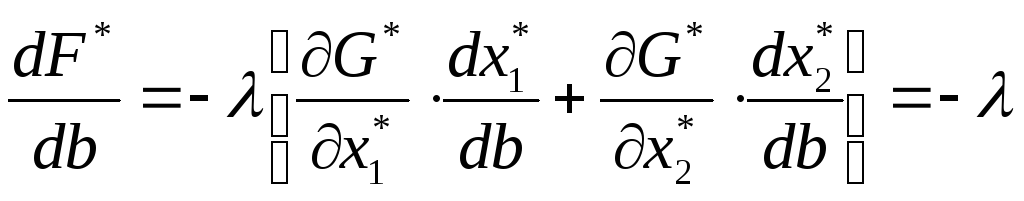(20)

Из (20) следует, что множитель Лагранжа характеризует "реакцию" значения на изменения параметра .

В общем случае (20) принимает вид: ; .

Таким образом, множитель , характеризует изменение оптимального при изменении соответствующего -того ресурса b_i на единицу.