6. Понятие локального (глобального), условного (безусловного) экстремума.

Теорема 1. Пусть – выпуклое множество из , функция 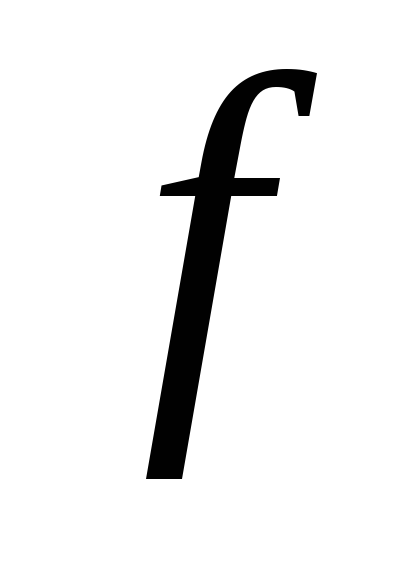– выпукла на . Тогда всякий локальный условный минимум функции на множестве является и глобальным.

Доказательство. Пусть – точка локального минимума функции на множестве . Тогда существует такое число , что для всех выполняется неравенство

. (1)

(Здесь .) Предположим

противное, то есть, что существует точка

такая, что

. (2)

В силу выпуклости множества имеем

. Следовательно,

для достаточно

малых значений . Из неравенств (1), (2) и в силу выпуклости функции на множестве для таких имеем

Полученное противоречие доказывает теорему.

Теорема 4. (Критерий условного экстремума в терминах конусов условно релаксационных направлений) Пусть – выпуклое множество из , функция 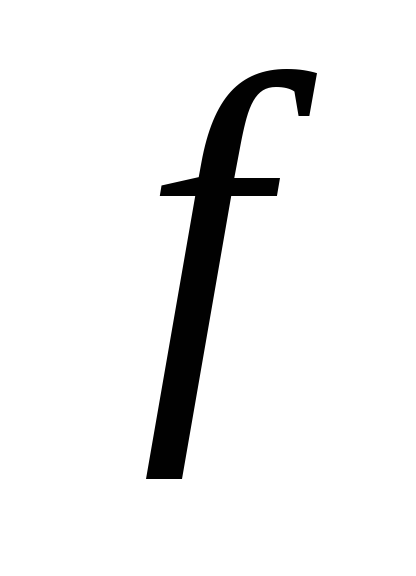выпукла на . Тогда для того, чтобы точка была минимумом функции на множестве , необходимо и достаточно, чтобы .

Доказательство. Необходимость. Пусть –минимум функции на . Убедимся, что конус

. Предположим противное, то есть

существует вектор . Поскольку по определению , найдется число такое, что при всех имеем и . Таким образом, получено противоречие с тем, что – условный минимум.

Достаточность. Пусть . Докажем, что . Предположим противное. Пусть существует точка такая, что

. (3).

Обозначим . Согласно теореме 5.4 имеем . Учитывая неравенство (3) и выпуклость функции , получаем неравенства справедливые при всех . Значит, . Таким образом, . Полученное противоречие доказывает теорему.

Следствие. Пусть функция выпукла на . Тогда для того, чтобы точка была безусловным минимумом функции , необходимо и

достаточно, чтобы .

Справедливость этого утверждения следует

из того, что здесь и (см. параграф 5).

Теорема 5. (Критерий условного экстрему-

ма первого порядка) Пусть – выпуклое множество, дифференцируемая функция выпукла на . Тогда для того, чтобы точка была минимумом функции на множестве ,

необходимо и достаточно, чтобы выполнялось условие

. (4)

Справедливость этого утверждения следует из теорем 4, 5.2 и 5.4.

Следствие. Пусть – выпуклая и дифференцируемая на функция. Тогда для того, чтобы точка была безусловным минимумом функции , необходимо и достаточно, чтобы .

Справедливость этого утверждения очевидным образом следует из (4) при .