Исследование функции
Ответ:
Чтобы исследовать функцию y = f(x) и построить ее график необходимо:
1) найти область определения функции, то есть множество всех точек для которых существует значение функции;
2) найти
(если они существуют) точки пересечения
графика с координатными осями. Для этого
нужно в уравнение 
подставить
аргумент 
а
также решить уравнение 
для
отыскания точек пересечения с осью 
;
3) исследовать функцию на периодичность, четность и нечетность. В некоторых случаях это можно сделать визуально по самому виду функции, если нет, то провести проверку:
1. 
–
функция четная;
2. 
–
функция нечетная;
3. 
–
функция периодическая, 
–
период функции.
Таким
образом, если имеем парную функцию
то
достаточно построить ее для положительных
значений 
,
после чего отразить ее симметрично
относительно оси абсцисс на другую
часть. В случае нечетной функции график
будет симметричен относительно начала
координат. Например, если имеет нечетную
функцию график которой принадлежит
первой четверти вторую половину получим
поворотом первой четверти на 180 градусов
(третья четверть).
Периодическими являются преимущественно функции, составленные из простых тригонометрических и некоторые параметрически заданные функции.
4) найти точки разрыва и исследовать их (такими точками являются края интервалов определения функции);
5) найти интервалы монотонности, точки экстремумов и значения функции в этих точках;
6) найти интервалы выпуклости, вмятины и точки перегиба;
7) найти асимптоты кривой;
8) построить график функции.
1)
Функция определена по всюду кроме точки,
в которой знаменатель превращается в
ноль (
).
Область определения состоит из двух
интервалов
2) При подстановке значения получим
Такую же точку получим если приравняем функцию к нулю. Точка - единственная точка пересечения с осями координат.
3) Проверяем функцию на четность
Итак функция ни четная, ни нечетная, непериодическая.
4) В данном случае имеем одну точку разрыва . Вычислим границы слева и справа от этой точки
Итак – точка разрыва второго рода.
5) Для отыскания интервалов монотонности вычисляем первую производную функции
Приравнивая
ее к нулю получим точки подозрительные
на экстремум 
.
Они разбивают область определения на
следующие интервалы монотонности
Исследуем поведение производной слева и справа от найденных точек разбиения
Графически интервалы монотонности будут иметь вид
Исследуемая
функция возрастает на интервалах 
и
убывает 
.
Точка
–
точка локального максимума, 
–
локального минимума. Найдем значение
функции
6) Для отыскания интервалов выпуклости найдем вторую производную
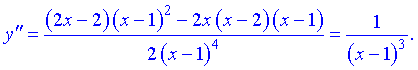
Таких интервалов нет, поскольку вторая производная не принимает нулевых значений в области определения.
7) Точка – вертикальная асимптота функции. Уравнение наклонной асимптоты имеет вид
где 
-
границы которые вычисляются по правилу
Находим нужные границы
Конечный вид прямой следующий
8) На основе проведенного анализа выполняем построение графика функции. Для этого сначала строим вертикальные и наклонные асимптоты, затем находим значение функции в нескольких точках и по них проводим построение.
