РЯДЫ
§ 7.	Положительные числовые ряды……………………………….	100
§ 8.	Знакочередующиеся и знакопеременные ряды……………….	117
§ 9.	Степенные ряды………………………………………………..	128
§ 10.	Разложение функций в степенные ряды……………………..	148
§ 11.	Ряды Фурье………………..……………………………………	163

Р Я Д Ы

§ 7. Положительные числовые ряды

1. Числовая последовательность

Определение 1. Если каждому значению 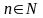по определенному правилу или закону поставлено в соответствие некоторое вещественное число 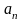, то множество занумерованных вещественных чисел 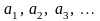называется числовой последовательностью (или последовательностью), обозначается символом 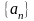, числа называются членами последовательности, а выражение называется общим членом последовательности.

Определение 2. Последовательность называется возрастающей (убывающей), если .

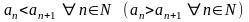Определение 3. Последовательность называется ограниченной сверху (ограниченной снизу), если существует такое число 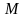(числ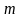о ), что

.

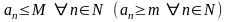Определение 4. Последовательность называется ограниченной, если она ограничена как снизу, так и сверху, то есть существуют такие числа и , что .

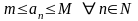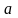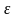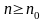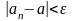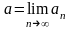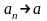Определение 5. Число называется пределом последовательности , если для любого сколь угодно малого положительного числа найдется такой номер , зависящий от , что для всех натуральных чисел выполняется неравенство . При этом последовательность называют сходящейся к числу и пишут: (или при ),

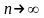Cвойства сходящихся последовательностей:

• Если последовательность имеет предел, то этот предел единственный;

• если последовательность имеет конечный предел, то она ограничена;

• если последовательность возрастает (убывает) и ограничена сверху (снизу), то она имеет конечный предел;

• если последовательность возрастает (убывает) и не ограничена сверху (снизу), то она имеет бесконечный предел .

2. Числовые ряды: основные понятия

Определение 6. Выражение

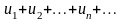, (1)

где – некоторые числа, называется числовым рядом (или просто рядом) и обозначается символом . При этом числа называются членами ряда, а выражение – общим членом ряда (1).

Определение 7. Сумма первых 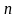членов ряда (1) называется -й частичной суммой ряда и обозначается .

Таким образом, числовому ряду (1) можно поставить в соответствие числовую последовательность 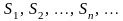( то есть ), называемую последовательностью частичных сумм ряда (1), где -й член последовательности задается формулой:

……………………

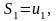
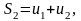
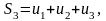
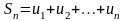. . (2)

Определение 8. Числовой ряд (1) называется сходящимся, если существует конечный предел 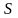последовательности его частичных сумм (2), то есть если 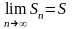. При этом число называется суммой ряда (1).

Определение 9. Если последовательность не имеет конечного предела, то ряд (1) называется расходящимся.

3. Необходимый признак сходимости ряда

Теорема 1. Если ряд (1) сходится, то предел его общего члена при равен нулю:

. (3)

Замечание 1. Условие (3) не является достаточным для сходимости ряда (1), а только необходимым.

Замечание 2. Из теоремы 1 рассуждением от противного получим достаточный признак расходимости числового ряда (1): если общий член ряда удовлетворяет условию

, (4)

то ряд (1) расходится. Однако, если ряд (1) расходится, то не обязательно имеет место условие (4).