6. Производная сложной функции

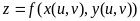Т е о р е м а 4. Пусть функции дифференцируемы в некоторой точке а функция дифференцируема в соответствующей точке Тогда сложная функция , как функция переменных и дифференцируема в точке и ее частные производные в этой точке вычисляются по формулам:

(4)

З а м е ч а н и е 6. Для случая функций большего (чем два) числа переменных формулы (4) обобщаются естественным образом. Например, если

где то имеют место аналогичные равенства:

П р и м е р 8. Вычислить если где

Р е ш е н и е. Находим:

Тогда по формулам вычисления частных производных сложной функции получаем:

О т в е т:

7. Полная производная

Т е о р е м а 5. Пусть функции дифференцируемы в некоторой точке , а функция дифференцируема в соответствующей точке Тогда сложная функция , как функция одной переменной , дифференцируема в точке и ее так называемая полная производная в этой точке вычисляется по формуле:

.

С л е д с т в и е. Пусть функция дифференцируема в некоторой точке , а функция дифференцируема в соответствующей точке , где . Тогда сложная функция , как функция переменной , дифференцируема в точке и ее полная производная в этой точке вычисляется по формуле:

Пример 9. Найти полную производную , если и , . Решение. В данном случае

, , , .

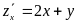Поэтому, воспользовавшись формулой вычисления полной производной, находим:

_Ответ:

П р и м е р 10. Найти (частную производную) и (полную производную), если где

Р е ш е н и е. Вычисляем:

Поэтому находим полную производную:

О т в е т:

8. Полный дифференциал

О п р е д е л е н и е 15. Полным дифференциалом функции в точке называется выражение вида:

(5)

где и независимые переменные.

З а м е ч а н и е 7 (свойство инвариантности формы полного дифференциала). Формула (5) справедлива и в случае, когда зависимые переменные.

Например, пусть , где независимые переменные. В этом случае полный дифференциал функции в точке , где вычисляется по формуле (5) , причем

где

З а м е ч а н и е 8. Правила дифференцирования функции одной переменной сохраняют силу и для функции любого числа переменных. Например, от скольких бы аргументов не зависели функции и справедливы равенства:

З а м е ч а н и е 9. В точке с точностью до бесконечно малых слагаемых высшего порядка относительно можно приближенно считать: то есть

П р и м е р 11. Найти полный дифференциал функции

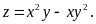
Р е ш е н и е. Предварительно находим: Тогда, воспользовавшись формулой (5), вычисляем

О т в е т:

Пример 12. Найти полный дифференциал функции

Решение. В данном случае , . Поэтому по формуле (5) находим: .

Ответ: .

П р и м е р 13. Вычислить приближенно число

Р е ш е н и е. Рассмотрим функцию Пусть Тогда Вычисляем:

Следовательно, по свойству дифференциала верно приближенное равенство:

О т в е т: