3. Функция, график
О п р е д е л е н
и е 10.
Если для
любой точки
из
множества
по некоторому правилу или закону
поставлено в соответствие определенное
число
из множества
то говорят, что на множестве
задана функция
п
переменны
.
При этом множество
называется областью
определения
функции
и обозначается
,
а множество
из
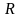называется множеством
значений
функции
и обозначается
.
О п р е д е л е н
и е 11.
Частным
значением
функции
в точке
называется число
равное
.
О п р е д е л е н
и е 12.
Графиком
функции
называется множество точек в
с координатами
где
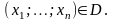
О п р е д е л е н
и е 13.
Линией
уровня
функции
двух переменных называется множество
точек плоскости
в каждой из которых функция
принимает одно и то же значение:
где
З а м е ч а н и е.
Аналогичное
понятие вводится для функции любого
числа
переменных. Однако в этом случае вместо
термина «линии уровня» используют
термин «поверхности
уровня».
4. Примеры с решениями
П р и м е р 1.
Площадь прямоугольника со сторонами
и
выражается формулой:
Поэтому
функция
двух переменных. Для нее областью
определения является множество
точек
,
у которых
(рис. 4). Множество значений функции:
у 
О х Рис. 4
П р и м е р 2.
Функция
функция двух переменных
и
Область ее определения
часть плоскости, заштрихованная на рис.
5, для любой точки
которой выполняется неравенство:
Множество значений функции:
у
2
О
х
Рис.
5
П р и м е р 3.
Функция
функция
двух переменных, для которой
Графиком функции является круговой
параболоид в пространстве
(рис. 6) с вершиной в точке
.
z
Y
О
х Рис. 6
П р и м е р 4.
Функция
функция трех переменных
Ее область определения
множество точек трехмерного пространства,
координаты которых удовлетворяют
неравенству:
.
Следовательно,
область определения – замкнутый шар
в
с центром в начале координат радиуса
– множество значений функции.
П р и м е р 5.
Найти значение функции
в точке
Р е ш е н и е.
Подставив
в выражение функции
,
получим:
О т в е т: 3.
П р и м е р 6. Найти область определения функции
Р е ш е н и е. Рассматриваемая функция определена и принимает действительные значения при выполнении системы неравенств:
Заменив знаки
неравенств знаками равенств, получим
уравнения границ области определения
функции z:
или
то есть
или
Таким образом,
граница области
состоит из двух окружностей с центрами
в начале координат и радиусами
Координаты внутренних точек области должны удовлетворять системе неравенств:
Точки, удовлетворяющие
неравенству (1), расположены вне окружности
Точки, чьи координаты удовлетворяют
неравенству (2), лежат внутри круга,
ограниченного окружностью
Одновременно неравенства (1) и (2) выполняются для точек плоскости, расположенных внутри кольца, ограниченного полученными окружностями (рис. 7). Причем внешняя граница этого кольца не принадлежит области , а внутренняя принадлежит.
у
D
О 2 3 х
Рис. 7
О т в е т: рис. 7.
П р и м е р 7.
Построить линии уровня функции
Р е ш е н и е.
Рассмотрим уравнение
откуда находим:
семейство
линий уровня.
Придавая числу
различные значения, определяем
соответствующие этому числу линии
уровня: ось Ох
за исключением точки О
(0; 0)
линия уровня
;
парабола
за исключением О
(0; 0) – линия уровня
И так далее (см. рис. 8).
у
с=2
с=1
с=0
О
х
с=1
с=2
Рис. 8
О т в е т: рис. 8.
П р и м е р 8. Найти поверхности уровня функции:
.
Р е ш е н и е. Рассматривая уравнение
,
получаем при различных значениях постоянной семейство поверхностей уровня данной функции.
● При
имеем:
– плоскость, проходящая через начало
координат;
● при
имеем:
– плоскость, параллельная первой и
пересекающая оси
,
,
в точках
,
,
соответственно;
● при
имеем:
– плоскость, параллельная предыдущим
и пересекающая оси
,
,
в точках
,
,
соответственно.
z
O
y
x Рис. 9
О т в е т: семейство параллельных плоскостей (рис. 9).