6. Интеграл эйлера – пуассона
О
п р е д е л е н и е 5. Несобственный
интеграл
называется интегралом
Эйлера–Пуассона.
Т
е о р е м а 6.
Интеграл
Эйлера–Пуассона существует и равен
числу
,
то есть имеет место равенство:
.
7. Приложения двойного интеграла
Площадь плоской области вычисляется по формуле:
.
Если область
определена неравенствами
,
,
то
.
Если область
определена неравенствами
,
,
то
.
Если область
в полярных координатах определена
неравенствами
,
,
то
.
Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью
,
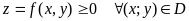снизу областью
на плоскости
,
сбоку цилиндрической поверхностью,
параллельной оси Оz,
вычисляется по формуле:
.
Площадь поверхности вычисляется по формуле:
где – проекция данной поверхности на плоскость .
Масса вещества (пластины), занимающего область плоскости и имеющего плотность
,
вычисляется по формуле:
.
При этом статические моменты пластины относительно осей и вычисляются по формулам:
,
.
Координаты центра тяжести пластины вычисляются по формулам:
,
.
В случае однородной
пластины
координаты центра тяжести вычисляются
по формулам:
,
.
П р и м е р 11. Найти площадь фигуры ограниченной линиями:
Р е ш е н и е. Область изображена на рис. 23. Она является правильной в направлении оси Ох и удовлетворяет теореме 3.
у у=х+2
2
D
О 4 х
-2
Рис. 23
Поэтому получаем:
О т в е т:
П р и м е р 12.
Найти площадь
той части конуса
,
которая заключена внутри цилиндра
.
Р е ш е н и е. Вычислим:
Тогда площадь поверхности вычисляется с помощью двойного интеграла:
,
где
областью интегрирования
является круг с центром в точке (1;0)
радиуса
,
ограниченный окружностью
.
Поэтому получаем:
.
О
т в е т:
.
П р и м е р 13.
Найти координаты центра тяжести
однородной фигуры, ограниченной линиями
(рис. 24).
Р е ш е н и е. В данном примере фигура однородна. Поэтому координаты центра тяжести находим по формулам:
где
площадь области
.
у
2
1 O 2 x
2
Рис. 24
Учитывая симметрию фигуры относительно оси , вычислим:
;
Следовательно,
О т в е т:
.