§ 7. Экстремумы функции

1. Экстремум

Пусть дана функция где , определенная на некотором множестве

О п р е д е л е н и е 1. Точка называется точкой максимума (минимума) функции если в области D существует такая окрестность с центром в точке во всех точках которой выполняется неравенство:

для всех точек отличных от и принадлежащих этой окрестности.

О п р е д е л е н и е 2. Точки максимумов и минимумов функции называются ее точками экстремумов (локальных экстремумов).

Т е о р е м а 1 (необходимое условие экстремума). Пусть функция где , определена в точке и имеет в ней экстремум. Если при некотором 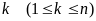в точке существует частная производная , то она равна нулю:

С л е д с т в и е 1. Если функция где в точке экстремума дифференцируема, то в этой точке в с е частные производные первого порядка данной функции равны нулю:

, … , .

С л е д с т в и е 2. Если функция где дифференцируема в точке экстремума , то

З а м е ч а н и е 1. Функция может иметь экстремум в точке , в которой хотя бы одна из частных производных первого порядка не существует, а существующие  равны нулю.

З а м е ч а н и е 2. Теорема 1 не является достаточной.

О п р е д е л е н и е 3. Точки области , в которых

или не существует,

. . . . . . . . . .

или не существует,

называются критическими (или стационарными) точками функции

З а м е ч а н и е 3. Если функция достигает экстремума в некоторой точке то эта точка является для функции критической. Однако не любая критическая точка функции является ее точкой экстремума.

О п р е д е л е н и е 4. Критическая точка функции, не являющаяся ее точкой экстремума, называется седловой точкой.

Т е о р е м а 2 (достаточные условия экстремума). Пусть функция где дважды непрерывно дифференцируема в окрестности точки Если для квадратной матрицы порядка вида

где (1)

все главные диагональные миноры положительные, то точка минимума функции Если все главные диагональные миноры матрицы положительные, то точка максимума функции Если все главные диагональные миноры матриц и не равны нулю, но нарушены описанные выше правила согласования их знаков, то седловая точка функции

З а м е ч а н и е 4. В теореме 2 матрица является симметричной: так как , откуда

Расшифруем условия теоремы 2:

• Если (2)

то точка м и н и м у м а;

• Если , (3)

то точка м а к с и м у м а;

• Если но не выполнены требования (2) или (3), то с е д л о в а я точка.

Как частный случай, сформулируем теорему 2, когда

Т е о р е м а 3 (достаточные условия экстремума функции двух переменных). Пусть функция определена в области и дважды непрерывно дифференцируема в окрестности критической точки Если выполняются неравенства

и (4)

то точка минимума функции Если выполняются неравенства

и (5)

то точка максимума функции Если выполняется неравенство

(6)

то седловая точка функции

З а м е ч а н и е 5. Теорема 3 не дает ответа на вопрос о принадлежности критической точки к точкам экстремума, если и В таких ситуациях требуется дополнительное исследование функции (по ее производным более высокого порядка, чем второй).

З а м е ч а н и е 6. Из теоремы 2 получаем следующее правило отыскания экстремума дважды непрерывно дифференцируемой функции.