О Г Л А В Л Е Н И Е

Функции нескольких переменных

	§ 3.		Понятие функции. График. Линии и поверхности уровня…..		34
	§ 4.		Предел. Непрерывность. Дифференцируемость……………		46
	§ 5.		Производные и дифференциалы высших порядков………..		60
	§ 6.		Производная по направлению. Градиент……………………		66
	§ 7. § 8.		Экстремумы функции………………………………………… Условный экстремум…………………………………………...		75 82
§ 9. § 10.		Двойной интеграл……………………………….………….….. Тройной интеграл……………………………….………….…..		91 110

Функции нескольких переменных § 3. Понятие функции. График. Линии и поверхности уровня

1. Пространство r n. Множества в Rn

О п р е д е л е н и е 1. Пространством n измерений называется множество упорядоченных групп из действительных чисел,

С геометрической точки зрения отождествляют с множеством точек вида Числа называют координатами точки; число размерностью пространства.

В пространстве определено расстояние (или между любыми двумя точками и вычисляется по формуле:

О п р е д е л е н и е 2. Множеством в пространстве называется любая часть этого пространства.

О п р е д е л е н и е 3. Открытым (замкнутым) шаром в с центром в точке радиуса называется множество точек удовлетворяющих условию:

О п р е д е л е н и е 4. Окрестностью точки называется любой открытый шар с центром в этой точке. Используют обозначение: где радиус шара.

О п р е д е л е н и е 5. Точка называется внутренней точкой множества , если она входит в вместе с некоторой своей окрестностью. Точка называется граничной точкой множества , если в любой ее окрестности есть точки как принадлежащие , так и не принадлежащие .

О п р е д е л е н и е 6. Множество называется открытым, если все его точки  внутренние. Множество , полученное из присоединением всех его граничных точек, называется замкнутым.

О п р е д е л е н и е 7. Множество называется ограниченным, если его можно заключить внутрь некоторого шара.

О п р е д е л е н и е 8. Множество называется односвязным, если любые его две точки можно соединить непрерывной кривой, все точки которой принадлежат

О п р е д е л е н и е 9. Областью в называется любое односвязное открытое множество в . Замкнутой областью в называется замкнутое множество, полученное из области присоединением всех ее граничных точек.

2. Прямоугольные и криволинейные координаты

В пространстве положение точки можно охарактеризовать различными наборами из чисел в зависимости от того, какая система координат используется. Например, введем в вместо прямоугольных координат какие-нибудь новые координаты по формулам:

(или

Если зафиксировать значение и считать переменной, то по указанным формулам получим некоторое семейство линий на плоскости Аналогично, если зафиксировать значение , считая переменной, получим другое семейство линий на плоскости

Линии указанных семейств называются координатными линиями в системе координат При этом положение точки определяется парой где и называемой криволинейными координатами точки Линии этих двух семейств могут быть как кривыми линиями, так и прямыми линиями. В точке координатные оси и выбирают на касательных к соответствующим координатным линиям. Орты этих координатных осей обозначают обычно

Система координат называется ортогональной криволинейной системой координат, если в любой точке плоскости координатные линии ортогональны, то есть

Например, в полярной системе координат

расстояние от полюса до точки

угол между полярной осью и лучом

Связь между прямоугольными координатами и полярными координатами точки задается формулами: В этом случае любая точка находится на пересечении двух координатных линий: (то есть окружности с центром в точке радиуса ) и (то есть луча, проходящего через точку и выходящего из полюса ). Полярная система координат является ортогональной (см. рис. 1).

M₀

φ₀

O 

Рис. 1

Аналогично вводятся криволинейные координаты в . Пусть вместе с прямоугольными координатами 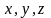положение точки определено тройкой криволинейных координат, связанных с формулами: (или

Множество точек пространства , для которых фиксирована одна из координат , называется координатной поверхностью системы координат Множество точек из , для которых фиксированы две из координат , называется координатной линией системы координат Система координат называется ортогональной, если в любой точке пространства координатные линии ортогональны.

_{Любая точка} находится на пересечении трех координатных поверхностей (то есть или трех координатных линий. В точке координатные оси выбирают на касательных к соответствующим координатным линиям. Орты этих координатных осей обозначают обычно