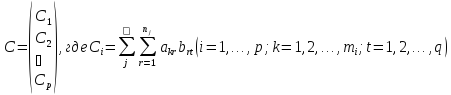Национальный Исследовательский Университет
МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
Институт автоматики и вычислительной техники
Кафедра прикладной математики
Лабораторная работа № 1
Умножение двух матриц
методом статического разделения на полосы
Курс «Параллельные системы и параллельные вычисления»
Выполнил
студент 5 курса группы А-13-08
Захаров Антон
Преподаватель
Панков Николай Александрович
Постановка задачи
Пусть даны две прямоугольные матрицы
 и
и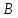 размерности
размерности и
и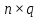 соответственно:
соответственно:

Требуется найти матрицу
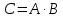 (произведением) размерности
(произведением) размерности :
:
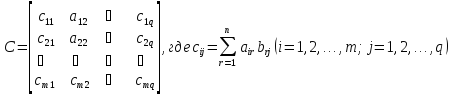
Для нахождения произведения матриц методом статического разделения на полосы необходимо составить последовательно-параллельную программу на языке C/C++ с применением интерфейса передачи сообщений (MPI,MessagePassingInterface), а также исследовать характеристики разработанной программы в зависимости от числа исполнителей.
Последовательный алгоритм решения
Умножение матриц по определению
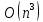
В соответствии с определением, произведение
матриц
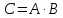 состоит из всех возможных комбинаций
скалярных произведений строк матрицы
состоит из всех возможных комбинаций
скалярных произведений строк матрицы и столбцов матрицы
и столбцов матрицы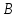 .
Элемент матрицы
.
Элемент матрицы с индексами (i, j) есть скалярное произведение
i-ой строки матрицы
с индексами (i, j) есть скалярное произведение
i-ой строки матрицы и j-го столбца матрицы
и j-го столбца матрицы .
.
for (i = 0; i < m; i++) {
for (j = 0; j < q; j++) {
C[i][j] = 0;
for (k = 0; k < n; k++)
C[i][j] += A[i][k] * B[k][j];
}
}
На первый взгляд это минимальный объем работы, необходимый для перемножения двух матриц. Однако исследователям не удалось доказать минимальность, и в результате они обнаружили другие алгоритмы, умножающие матрицы более эффективно.
Алгоритм Штрассена
Первый алгоритм быстрого умножения матриц был разработан В. Штрассеном в 1969. В основе алгоритма лежит рекурсивное разбиение матриц на блоки. Недостатком данного метода является большая сложность программирования по сравнению со стандартным алгоритмом, численная неустойчивость и большой объём используемой памяти.
Разработано большое количество алгоритмов на основе метода Штрассена, которые улучшают его численную устойчивость и уменьшают объём используемой памяти.
Алгоритм
Копперсмита-Винограда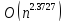
В 1990 Копперсмит и Виноград опубликовали
алгоритм, умножающий матрицы со сложностью
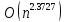 .
Этот алгоритм использует идеи, схожие
с алгоритмом Штрассена. На сегодняшний
день алгоритм Копперсмита-Винограда
является наиболее асимптотически
быстрым, но он эффективен только на
очень больших матрицах и поэтому не
применяется.
.
Этот алгоритм использует идеи, схожие
с алгоритмом Штрассена. На сегодняшний
день алгоритм Копперсмита-Винограда
является наиболее асимптотически
быстрым, но он эффективен только на
очень больших матрицах и поэтому не
применяется.
В 2003 Кох и др. рассмотрели в своих работах
алгоритмы Штрассена и Копперсмита-Винограда
в контексте теории групп. Они показали
возможность существования алгоритмов
умножения матриц со сложностью
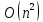 .
.
Параллельный алгоритм решения
В предлагаемой реализации метода
статического разделения на полосы
исходные матрицы разбиваются на
горизонтальные полосы. Получаемые
полосы распределяются по процессорам:
все полосы одной матрицы, например
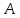 ,
распределяются между процессорами, а
полосы другой – по мере необходимости
передаются на все процессоры. При этом
на каждом из имеющегося набора процессоров
в каждый конкретный момент времени
располагается только по одной полосе
матриц
,
распределяются между процессорами, а
полосы другой – по мере необходимости
передаются на все процессоры. При этом
на каждом из имеющегося набора процессоров
в каждый конкретный момент времени
располагается только по одной полосе
матриц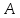 и
и .
Перемножение полос (а данная операция
может быть выполнена процессорами
параллельно) приводит к получению частей
(полос) результирующей матрицы
.
Перемножение полос (а данная операция
может быть выполнена процессорами
параллельно) приводит к получению частей
(полос) результирующей матрицы ,
которые затем в совокупности и дадут
искомую матрицу.
,
которые затем в совокупности и дадут
искомую матрицу.
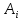 – полоса матрицы
– полоса матрицы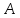 ;
;
 – полоса матрицы
– полоса матрицы ;
;
 – число процессоров.
– число процессоров.