Основные положения теории Дебая и Гюккеля

Дебай и Гюккель приняли основную идею Гхоша о кристаллоподобном распределении ионов в растворе. Однако в растворе ионы в результате теплового движения располагаются вокруг какого-то центрального иона в виде сферы. Так как в растворе преобладает поступательное движение (а не колебательное, как в кристаллах), ионы, входящие в состав сферы, окружающей центральный ион, непрерывно обмениваются своими местами с другими ионами. Такая статистическая сфера называется ионной атмосферой. Все ионы раствора равноценны, каждый из них окружен ионной атмосферой, и, в то же время, каждый центральный ион входит в состав ионной атмосферы какого-либо другого иона. Существование ионных атмосфер и есть тот характерный признак, который по Дебаю и Гюккелю отличает реальные растворы электролитов от идеальных.

В очень разбавленных растворах сильных электролитов можно условно считать, что взаимодействие между ионами целиком определяется электростатическими силами. Поэтому теория растворов электролитов Дебая и Гюккеля называется электростатической. Данная теория базируется на ряде допущений: Все молекулы электролита полностью распадаются на ионы

1. Ионы - точечные заряды (процессами сольватации можно пренебречь).

2. Можно пренебречь всеми видами взаимодействий в растворе, кроме электростатического взаимодействия иона с его ионной атмосферой.

3. Электростатическое поле иона и ионная атмосфера имеют шаровую симметрию.

4. Диэлектрическая проницаемость раствора равна диэлектрической проницаемости чистого растворителя (электролит не влияет на диэлектрические свойства).

Потенциал вокруг иона (согласно теории Дебая и Гюккеля) складывается из потенциала иона и потенциала ионной атмосферы ,

Для точки r, расположенной на расстоянии r от центрального иона, его потенциал (кулоновский потенциал) с учетом диэлектрической проницаемости среды s определяется выражением

, (32.23)

где Ф/м - диэлектрическая постоянная вакуума (электрическая постоянная). Таким образом, в растворе чисто кулоновский потенциал понижается в s раз по сравнению с его величиной для изолированного иона в вакууме.

Второй эффект в растворе вызван наличием ионной атмосферы. Установлено, что потенциал уменьшается с расстоянием r более резко, чем это предсказывает уравнение (32.23). Отмеченное обусловлено наличием слабого противоположного заряда ионной атмосферы, которая притягивается к центральному иону. В такой ситуации говорят, что центральный заряд экранирован, и соответствующий потенциал называется экранированным кулоновским потенциалом, для которого 1/r в уравнении (32.23) заменяется на где где параметр определяет, как сильно отличается этот потенциал от чисто куло-новского. Величина для рассматриваемой точки r представляет собой среднее значение потенциала, создаваемого в ней ионной атмосферой и центральным ионом, и определяется выражением

. (32.24)

Для реальных растворов специфическим является потенциал ионной атмосферы, который находят по правилу суперпозиции потенциалов как разность и . Для точки r его величина определяется выражением

(32.25)

Для вычисления энергии взаимодействия необходимо определить потенциал ионной атмосферы в точке нахождения центрального иона, т. е найти предел при , который определяется выражением

(32.26)

Величину в соответствии с уравнением (32.26) можно рассматривать как потенциал, создаваемый в точке нахождения центрального иона другим ионом с противоположным знаком, находящимся от центрального иона на расстоянии Величина называется характеристической длиной ⁴(или радиусом) ионной атмосферы, под которым следует понимать то расстояние от центрального иона, на котором надо было бы разместить все заряды, входящие в ионную атмосферу, чтобы их суммарное влияние на центральный ион было бы равно суммарному влиянию существующей ионной атмосферы. Эта величина является условной, так как в действительности плотность заряда ионной атмосферы убывает монотонно, приближаясь к нулю. Практически на расстоянии плотность заряда ионной атмосферы становится пренебрежимо малой. Радиус ионной атмосферы рассчитывается по уравнению

, (32.27)

Где моль - постоянная Авогадро; число ионов в единице объема (1м ). Для удобства в это выражение вводят вместо молярную концентрацию ( моль/л) используя соотношение Тогда с учетом (32.20)

. (32.28)

Энергия Гиббса электростатического взаимодействия ионов рассчитывается по законам электростатики:

. (32.29)

Как уже отмечалось, работа, совершаемая системой в неидеальном состоянии, равна убыли термодинамического потенциала, т. е.

(32.30)

Зная потенциал ионной атмосферы в точке нахождения центрального

Иона можно, исходя из выражений (32.29) и (32.30), рассчитать работу W, на 1 моль электролита, которую необходимо затратить на разрушение ионной атмосферы:

(32.31)

Подставляя в это выражение значение из (32.25), имеем

. (32.32)

Выражение (32.32) в сочетании с (32.17) дает выражение для расчета коэффициента активности данного сорта ионов

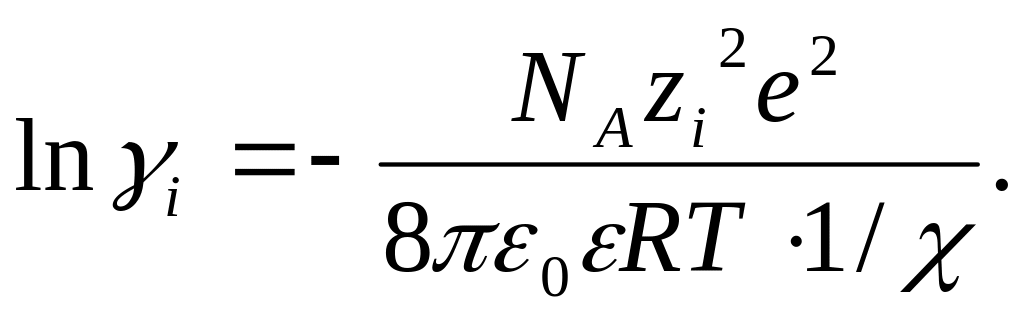(32.33)

Подстановка значения из (32.28) в (32.33) приводит к

(32.33а)

В большинстве случаев нужно знать также и средний коэффициент активности электролита , причем опытные данные позволяют найти именно эту величину. Рассмотренный выше материал позволяет рассчитать средний коэффициент активности для раствора электролита, образованного из соединения с общей формулой Из определения среднего коэффициента активности по аналогии с (32.19) для данного раствора электролита

получим или в логарифмическом виде:

(32.34)

Исходя из (32.34)

, и

Подставляя значения и в уравнение (32.34), после преобразований с учетом закона электронейтральности (32.1), перейдя к десятичным логарифмам и подставив значения постоянных величин, получим:

(32.35)

Обозначая через В, имеем

(32.36)

или для 1 -1 – электролитов

(32.37)

Уравнение (32.36) представляет собой предельный закон Дебая-Гюккеля, а коэффициент B называют предельным коэффициентом или коэффициентом предельного закона Дебая-Гюккеля. При 298K и диэлектрической постоянной раствора, равной диэлектрической постоянной воды B = 0,509.

Все допущения Дебая и Гюккеля приводят к тому, что предельный закон Дебая и Гюккеля, называемый также первым приближением теории Дебая и Гюккеля, справедлив лишь по отношению к разбавленным растворам электролитов с ионами низкой зарядности. В водных растворах он соблюдается лишь при ионной силе меньше Однако этот закон имеет большое значение, поскольку эмпирическая зависимость от получает теоретическое обоснование. Другими словами, в этом законе получило теоретическое обоснование правило ионной силы.

Во втором приближении теории Дебая и Гюккеля учитываются конечные размеры ионов с помощью параметра a и влияние других ионов на радиус рассматриваемого иона с помощью коэффициента b. Параметр a определяется как среднее расстояние при максимальном сближении ионов. Однако точное определение физического смысла этой величины для растворов электролитов затруднено. В связи с тем, что методы независимого определения параметра a не существуют, он часто рассматривается как эмпирическая константа, отражающая конечные размеры ионов. Уравнение второго приближения имеет вид

. (32.38)

Коэффициент b для воды при 298 K равен и сравнительно мало изменяется с температурой. Параметр a подбирают таким образом, чтобы рассчитанные по (32.38) коэффициенты активности совпадали с опытными. По порядку величины он близок к размеру ионов ( см). Уравнение (32.38) для водных растворов может быть применено вплоть до ионной силы 0,1. Для многих электролитов величина ионного параметра a оказывается равной см, т. е. . В этих случаях из (32.38) получаем уравнение

, (32.39)

применимое для растворов с ионной силой не более 0,05.

Для более широкой области изменения ионной силы растворов применяется уравнение

(32.40)

учитывающее уменьшение диэлектрической постоянной в непосредственной близости к иону. Коэффициент d - это поправка, учитывающая влияние растворенного электролита на диэлектрические свойства раствора и определяющаяся практически из экспериментальных данных по зависимости от концентрации. В концентрированных растворах может быть больше единицы, так как силы отталкивания могут превысить силы притяжения между ионами.