Национальный исследовательский институт

Московский Энергетический Институт (Технический Университет)

Институт автоматики и вычислительной техники

Кафедра Прикладной математики

Лабораторная работа №5

по дисциплине «Параллельные системы и параллельное программирование»

тема: «Программирование на языке FPTL»

Выполнил:

Машеров Д.Е.

А-13-08

Москва

2012 г.

Задачи

1. Реализовать алгоритм перемножения матриц. Матрицу представлять в виде списка списков.

2. Реализовать алгоритм поиска минимального остовного дерева (оптимального каркаса) методом Прима.

1. Перемножение матриц

Описание

Пусть даны две прямоугольные матрицы и размерности и соответственно:

Тогда матрица размерностью называется их произведением:

где:

Реализация.

Был создан тип «Список»(«List»), значениями которого могут быть

1. Пустой список (c_nil);

2. Пара: элемент любого типа и список из элементов этого типа.

Матрицы представляются в виде списка списков, считываются из файлов.

Чтение осуществляется функцией readMatrix, в которой используются функции readSize(размер матрицы в файле), readElements(элементы матрицы в файле) и readNumber( чтение числа в файле).

Умножение осуществляется функцией matrixMult, в которой используются функции rowMult (возвращает строку результирующей матрицы) и elemSum(возвращает элемент результирующей матрицы).

Результаты вычислительного эксперимента

Количество строк и столбцов обеих матриц: 100:

Число процессоров	Время решения, секунды
1	102.452
2	82.722
3	79.589
4	79.104
5	77.836
6	76.314
7	74.962
9	76.008

2. Поиск минимального остовного дерева (оптимального каркаса) методом Прима

Описание

Алгоритм начинает работу с произвольной вершины графа, выбираемой в качестве корня дерева, и в ходе последовательно выполняемых итераций расширяет конструируемое дерево до МОД. Пусть есть множество вершин, уже включенных алгоритмом в МОД, а величины 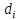, 1<= <=n, характеризуют дуги минимальной длины от вершин, еще не включенных в дерево, до множества 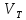, т.е.

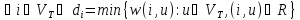
(если для какой-либо вершины не существует ни одной дуги в 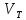, значение устанавливается равным ). В начале работы алгоритма выбирается корневая вершина МОД s и полагается ={s}, =0.

Действия, выполняемые на каждой итерации алгоритма Прима, состоят в следующем:

• определяются значения величин di для всех вершин, еще не включенных в состав МОД;

• выбирается вершина t графа G, имеющая дугу минимального веса до множества ;

• вершина t включается в VT.

После выполнения n-1 итерации метода МОД будет сформировано. Вес этого дерева может быть получен при помощи выражения

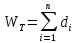
Реализация.

Был создан тип «Список»(«List») (см. реализацию перемножения матриц) и тип «Пара»(«Pair») – кортеж из двух элементов типа int.

Граф представляется матрицей смежности.

Матрицы представляются в виде списка списков, считываются из файлов.

Чтение осуществляется функциями readSize(размер матрицы в файле), readElements(элементы матрицы в файле) и readNumber( чтение числа в файле).

Умножение осуществляется функцией prims, в которой используются функции Iteration(итерация алгоритма Прима), checkForMin(ищет дугу с минималным весом для всех вершин остова), adjIteration(перебор вершин остова), adjCheckForMin (ищет дугу с минималным весом для одной вершины остова).

Результаты вычислительного эксперимента

200 вершин:

Число процессоров	Время решения, секунды
1	280.058
2	275.579
3	269.447
4	266.144
5	268.342
6	265.533
7	262.982
9	261.835