Основы информатики. Лаб14. Основной метод информатики 24 мая 2016

Задача об остывании кофе

Гулд Х., Тобочник Я. Компьютерное моделирование в физике. Том 1: М., изд-во Мир. – 1990г. : 352с.

2.1. Основные понятия

Знакомство с численными методами неплохо начать с того, что расположиться подальше от компьютера и насладиться чашечкой горячего кофе (или чая). Однако, отхлебнув из чашечки кофе, мы по обыкновению обжигаемся, поскольку он очень горячий. Если нам не терпится, то можно добавить в кофе молока. Но если после этого кофе все еще горячий, ничего не остается делать, как подождать некоторое время, пока он не остынет до нужной температуры. Если желательно, чтобы кофе остыл как можно быстрее, то что лучше — добавить молоко сразу после приготовления кофе или немного подождать, прежде чем добавлять молоко?

Природа переноса тепла от кофе к окружающему пространству сложна и в общем случае включает в себя механизмы конвекции, излучения, испарения и теплопроводности. В том случае, когда разность температур между объектом и окружающей средой не очень велика, скорость изменения температуры объекта можно считать пропорциональной этой разности температур. Это утверждение более строго можно сформулировать на языке дифференциального уравнения:

(2.1)

где Т — температура тела, Т_S — температура окружающей среды, а r — «коэффициент остывания». Этот «коэффициент остывания» зависит от механизма теплопередачи, площади тела, находящегося в контакте со средой и тепловых свойств самого тела. Знак минус появляется в (2.1) во избежание нефизического эффекта увеличения температуры тела, когда Т > Т_S. Соотношение (2.1) называется законом теплопроводности Ньютона. Попытайтесь проинтегрировать уравнение (2.1) и получить зависимость температуры от времени.

Уравнение (2.1) —пример дифференциального уравнения первого порядка, поскольку в него входит только первая производная неизвестной функции T(t). Ввиду того что множество процессов, происходящих в природе, описываются дифференциальными уравнениями, важно уметь решать эти уравнения. Рассмотрим уравнение первого порядка вида

(2.2)

В общем случае аналитического решения уравнения (2.2), выраженного через хорошо известные функции, не существует. Кроме того, даже в том случае, когда аналитическое решение все же существует, необходимо представить решение в графическом виде, чтобы понять его характер. Эти причины побуждают нас искать не точные, а приближенные численные решения дифференциальных уравнений и познакомиться с простыми методами графического представления решений.

2.2. Алгоритм эйлера

Типичный метод численного решения дифференциальных уравнений включает в себя преобразование дифференциального уравнения в конечно-разностное. Проанализируем уравнение (2.2). Положим, что при х = x₀ функция у принимает значение y₀. Поскольку уравнение (2.2) описывает изменение функции у в точке х₀, то можно найти приближенное значение функции у в близлежащей точке , если приращение аргумента мало. В первом приближении предполагается, что функция g(x), или скорость изменения у, постоянна на отрезке от x₀ до х₁ В этом случае приближенное значение функции у в точке определяется выражением

+ (2.3)

Мы можем повторить эту процедуру еще раз и найти значение у в точке ,:

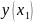+ (2.4)

Очевидным образом это правило можно обобщить и вычислить приближенное значение функции в любой точке по итерационной формуле

+ (n=0, 1, 2,…) (2.5)

Данный метод называется методом касательных, или методом Эйлера. Можно предположить, что метод будет давать хорошее приближение к «истинному» значению функции у, если приращение аргумента достаточно мало. Степень «малости» определяется нашими требованиями и может не конкретизироваться до тех пор, пока метод не применяется для решения конкретных задач.

В методе Эйлера предполагается, что скорость изменения функции у на отрезке от до х_п постоянна, а наклон касательной вычисляется в начальной точке отрезка. Графическая интерпретация выражения (2.5) приведена на рис. 2.1. Понятно, что в случае, когда наклон касательной меняется на некотором отрезке, появляется отклонение от точного решения. Тем не менее, это отклонение можно уменьшить, если выбрать меньшее значение .

Рис. 2.1. Графическая интерпретация метода Эйлера. Наклон касательной вычисляется в начальной точке интервала. Приближению Эйлера и истинной функции соответствуют прямая и кривая.