1.3 Випадок класів, які задаються обмеженнями на декілька похідних

Введемо класи

.

.

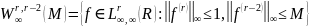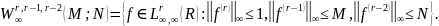
Нехай Визначимо T:= . Визначимо функцію наступним чином (див. [4], с. 2). На відрізку [0;T] покладемо

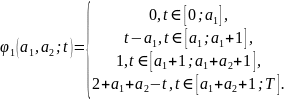
(див. рис.5)

Продовжимо функцію на відрізок [T;2T] рівнянням

а потім періодично із періодом на усю вісь.

Через , де будемо позначати сплайн Ейлера порядку r (тобто - ту періодичну первісну функції sgn(sin(t)) із середнім значенням нуль на періоді) (функції вперше розглядав Родов [8]).

1

-1

рис.5

Для , і 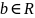покладемо

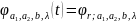(t):= .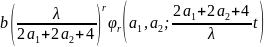

Відзначимо, що функція є - періодичною (див. [4], с. 3)

Теорема D. Нехай і . Нехай виконується одна із умов.

1. Числа , , λ і такі, що

,

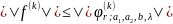-1

1

рис. 6

2. Числа , , λ і такі, що ,

-1

1

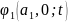
рис. 7

-1

1

рис. 8

3. Числа , , λ і такі, що

,

Тоді функція є функцією порівняння для функції .

-1

1

рис. 9

рис. 10

Зауваження. Попередня теорема демонструє, що при відповідному підборі параметрів , ; , ; функція буде функцією порівняння для функції f для класів відповідно.

Розділ 2. Функція та її властивості

2.1 Означення екстремальної функції

У даній роботі розглядається клас , на якому ми задамо несиметричний сплайн .

- клас усіх функцій f, які мають r-1 похідну, - локально абсолютно неперервна і , .

Нехай побудуємо функцію .

Нехай , 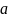- довільне, , .

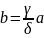(див. рис. 11)

0

-

t

y

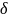
рис. 11

Продовжимо функцію періодично на всю вісь з періодом T= .

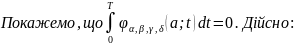
(2.3.1)

Розглянемо 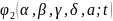, що є первісною з нульовим середнім на періоді. Тоді в силу (2.3.1) 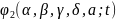, є також періодичною. Аналогічно для будь- якого r , 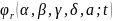- це первісна функції з нульовим середнім на періоді.

2.2 Деякі властивості екстремального сплайна

Відзначимо основні властивості .

З означення Оскільки

, звідси випливає, що

має два нулі на періоді і при r строго монотонна між точками локального екстремуму.

Лема. Нехай f належить простору .

Тоді : .

Доведення. В силу означення , , , при 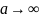. Тоді , таке, що

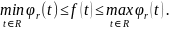
Розділ 3. Основні результати

Теорема. Якщо f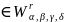 (R), і таке, що

для будь- якого , то функція 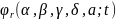є функцією порівняння для функції f(t).

Доведення. Скористаємось методом математичної індукції.

Далі для скорочення записів будемо писати замість .

Базис: Нехай r=1.

Доведемо, що якщо f і

то функція є функцією порівняння для функції f(t).

Позначимо .

Доведемо від протилежного. Нехай функція не є функцією порівняння для функції f(t). Можемо вважати, що проміжок монотонності функції , де функція неспадна і на цьому проміжку змінює знак з «-» на «+», тобто

, ( і (

Нехай 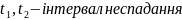функції , на якому функція змінює знак з «-» на «+».

Нехай ( , - проміжок строгої монотонності .

Оскільки 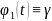на ( , і (R), то отримаємо

Оскільки на ( , і (R), то отримаємо .

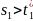Тоді ( ), отже ( .

.

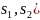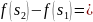
Отримали протиріччя з (3.2), отже є функцією порівняння для f у випадку r=1.

Індуктивне припущення. Нехай твердження справедливе при r=k-1, тобто, якщо і виконується

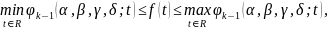
то функція 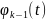є функцією порівняння для функції f(t).

Доведемо твердження при r=k. Нехай 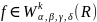і

Доведемо, що функція є функцією порівняння для функції f(t).

Для цього спочатку доведемо, що

Припустимо супротивне. Нехай (3.3) не виконується. Це можливо у наступних 3 випадках:

1 випадок:

2 випадок:

3 випадок: 0

Розглянемо 3 випадок, інші випадки розглядаються аналогічно.

Без зменшення загальності можемо вважати, що

(3.4)

Оскільки замість ми можемо розглянути функцію , де - число, будемо вважати, що

Нехай - найближчі ліворуч та праворуч від нулі функції , функція зростає на ( і спадає на ( .

В силу (3.1)

⇒ ( :0 ). Будемо вважати, що

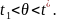
Розглянемо функцію

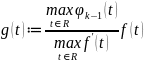, тоді g ,

.

і в силу (3.4)

Тобто, для g усі умови індуктивного припущення виконуються.

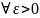розглянемо функцію h(t) h(t)=g(t+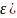 . В силу означення h для неї також виконуються умови з індуктивного припущення. Дійсно, h

крім того, h(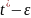 )=g( , враховуючи (3.6) можемо обрати настільки малим, щоб виконувалось h( тоді різниця змінює знак з «-» на «+», отже не є функцією порівняння для функції h, що суперечить індуктивному припущенню. Таким чином ми довели (3.3).

Повернемось до доведення індуктивного припущення.

Нехай r=k і f , така, що виконується (3.1). Тоді справедливі нерівності (3.3).

Розглянемо різницю .

Припустимо супротивне, що не є функцією порівняння для функції f,

Можемо вважати, що на проміжку зростання ,є зміни знаку функції з «-» на «+».

Нехай , - проміжок зростання і

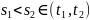
Розглянемо (t)=(1- f(t)- (t), де вибрано так, щоб

(

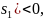
В силу (3.1)

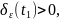
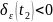(див. рис. 12).

A

B

C

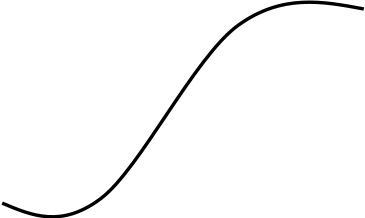
рис. 12

Тоді існують точки А, В, С:

і

(див. рис. 13).

A

C

B

рис. 13

можемо вважати, що дві з 3 точок лежать на ( , така, що зростає на ( і спадає на ( . Але тоді функція змінює знак з «-» на «+» на проміжку зростання ( функції , отже не є функцією порівняння для функції (1- f, що суперечить індуктивному припущенню. Теорема доведена.

ВИСНОВКИ

Дипломна робота присвячена отриманню аналогів теореми порівняння Колмогорова для класу функцій, що задаються обмеженнями на несиметричні норми старших похідних.

У першому розділі була розглянута теорема порівняння Колмогорова для різних класів.

У другому розділі була введена екстремальна функція та були доведені деякі її властивості.

У третьому розділі була доведена теорема порівняння для класу

(- ).

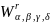ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ

[1] Корнейчук Н. П. Сплайны в теории приближений- М.: Наука. Главная редакция физико- математической литературы, 1984, 352 с., с. 64.

[2] Корнейчук Н. П Точные константы в теории приближения- М.: Наука . Гл. ред. физ.- мат. лит., 1987.-424 с., с. 94, с. 104, с. 119.

[3] Корнейчук Н. П. Экстремальные задачи теории приближения. Главная редакция физико- математической литературы изд- ва «Наука», М., 1976, с. 113.

[4] В. Ф. Бабенко, О. В. Коваленко Теоремы сравнения производных и некоторые их приложения. Вісник ДНУ, 2012,Том 1, №1, 1-9 ISSN 9128- 0912.

[5] В. Ф. Бабенко, Н. П. Корнейчук, В. А. Кофанов, С. А. Пичугов Неравенства для производных и их приложения, Киев, Наукова думка, 2003, с. 66, с. 69.

[6] Колмогоров А. Н. о неравенствах между верхними гранями последовательных производных произвольной функции на бесконечном интервале .// В кн. А. Н. Колмогоров, избранные труды, Математика и механика, М. Наука, 1985, с. 252- 263.

[7] Корнейчук Н. П., Бабенко В. Ф., Лигун А. А. Экстремальные свойства полиномов и сплайнов.- Киев. Наук. думка 1992, -304 с.

[8] Родов А. М. Зависимость между верхними гранями производных функций действительного переменного // Изв. АН СССР. Сер. Мат.- 1946. 10. с.- 257-270.

[9] Корнейчук Н. П., Лигун А. А., Доронин В. Г. Аппроксимация с ограничениями – Киев: Наукова думка, 1982,- 250 с.

[10] Babenko V. F., Kofanov V. A., Pichugov S. A. Inequalities for norms of intermediate derivatives of periodic functions and their applications// Ibid.- N 3.- P. 251- 376.